VAE and MLE
Now Im sure that all my VAE and ELBO related learning were NOT recorded in this blog. So it’s time to review some courses from Hung-yi.
1 Maximum Likelyhood Estimation
A good intuition about MLE is from StatQuest. A quick review before we jump into VAE. The likelihood of observation data is the key of this method.
The intuition is find a way to maximun such likelihood, by choosing a proper mean
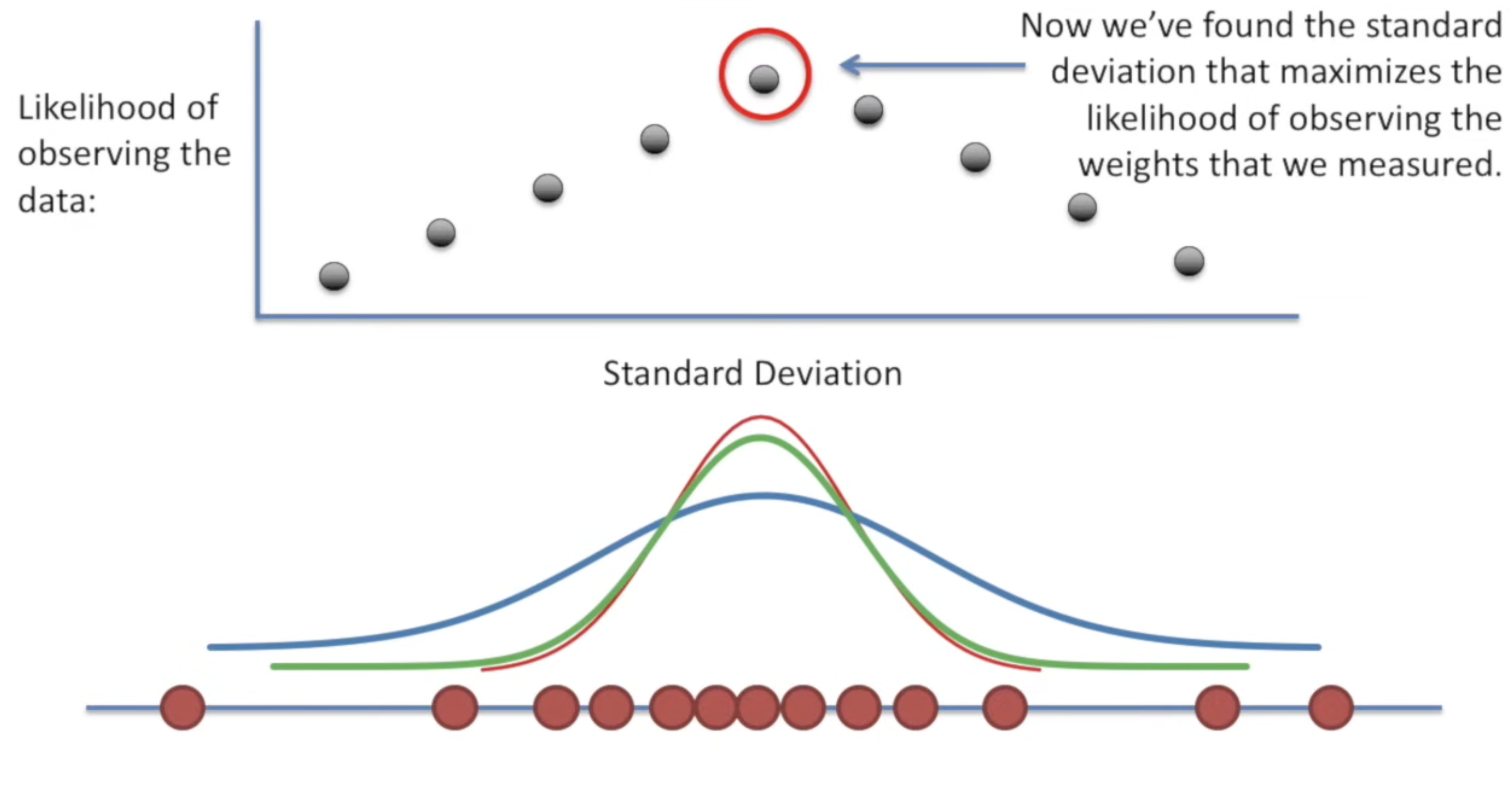
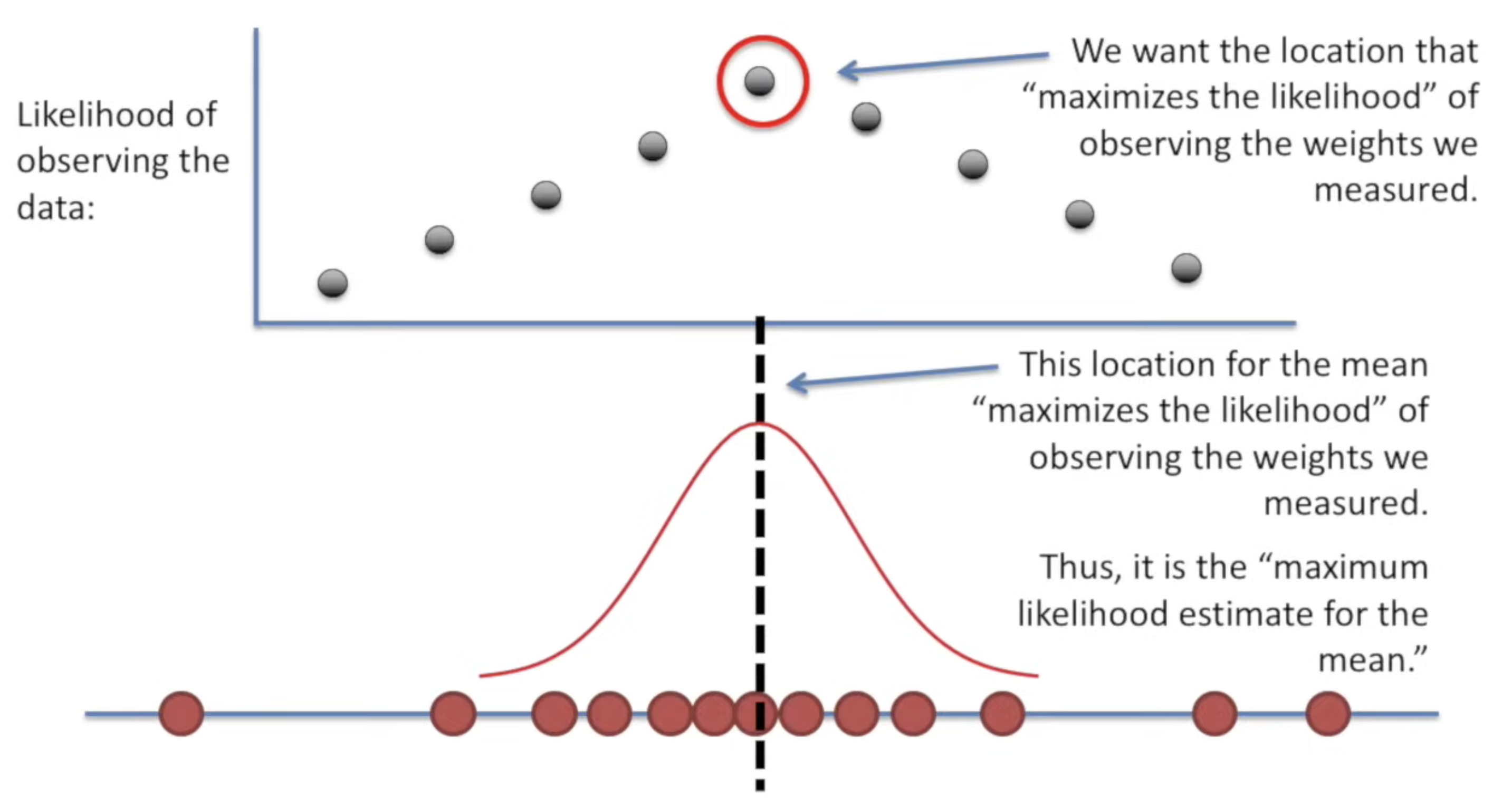 and choosing a proper variance
and choosing a proper variance
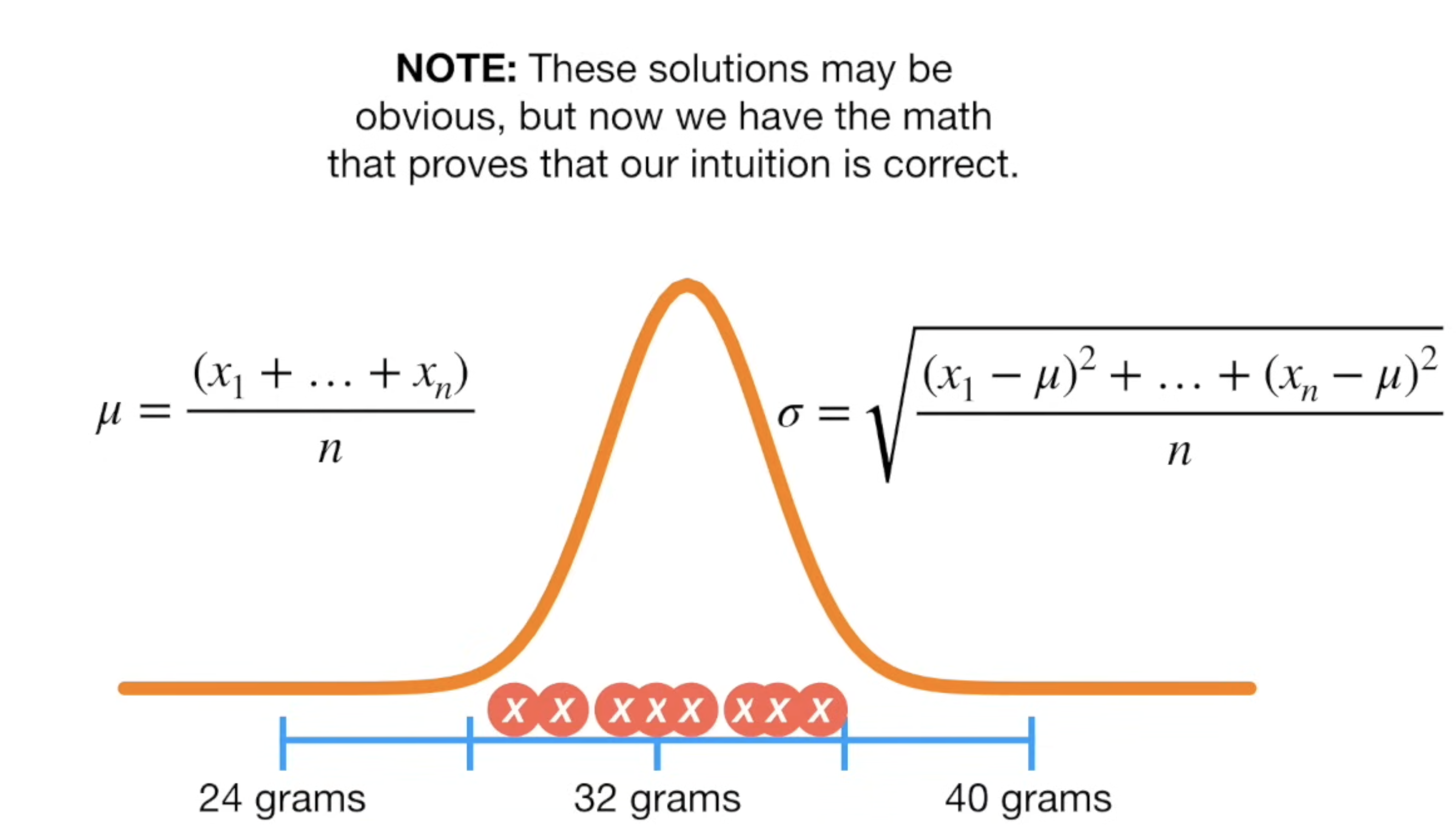
 Mathmatically, with a series of observed data, we can estimate the mean of the distribution
Mathmatically, with a series of observed data, we can estimate the mean of the distribution
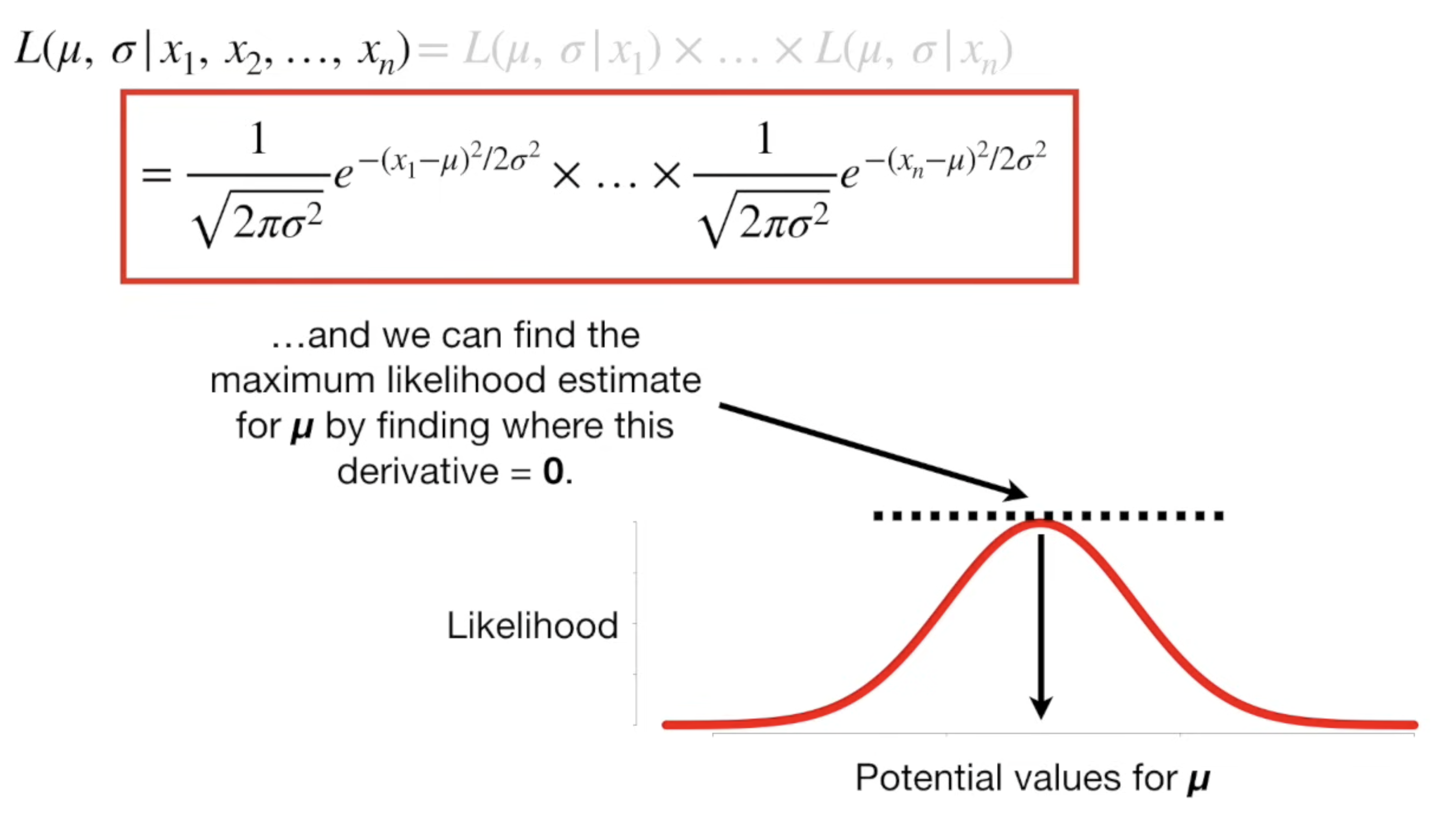 For mean, to make the derivate equals to zero, we have
For mean, to make the derivate equals to zero, we have
 For variance, we have
For variance, we have
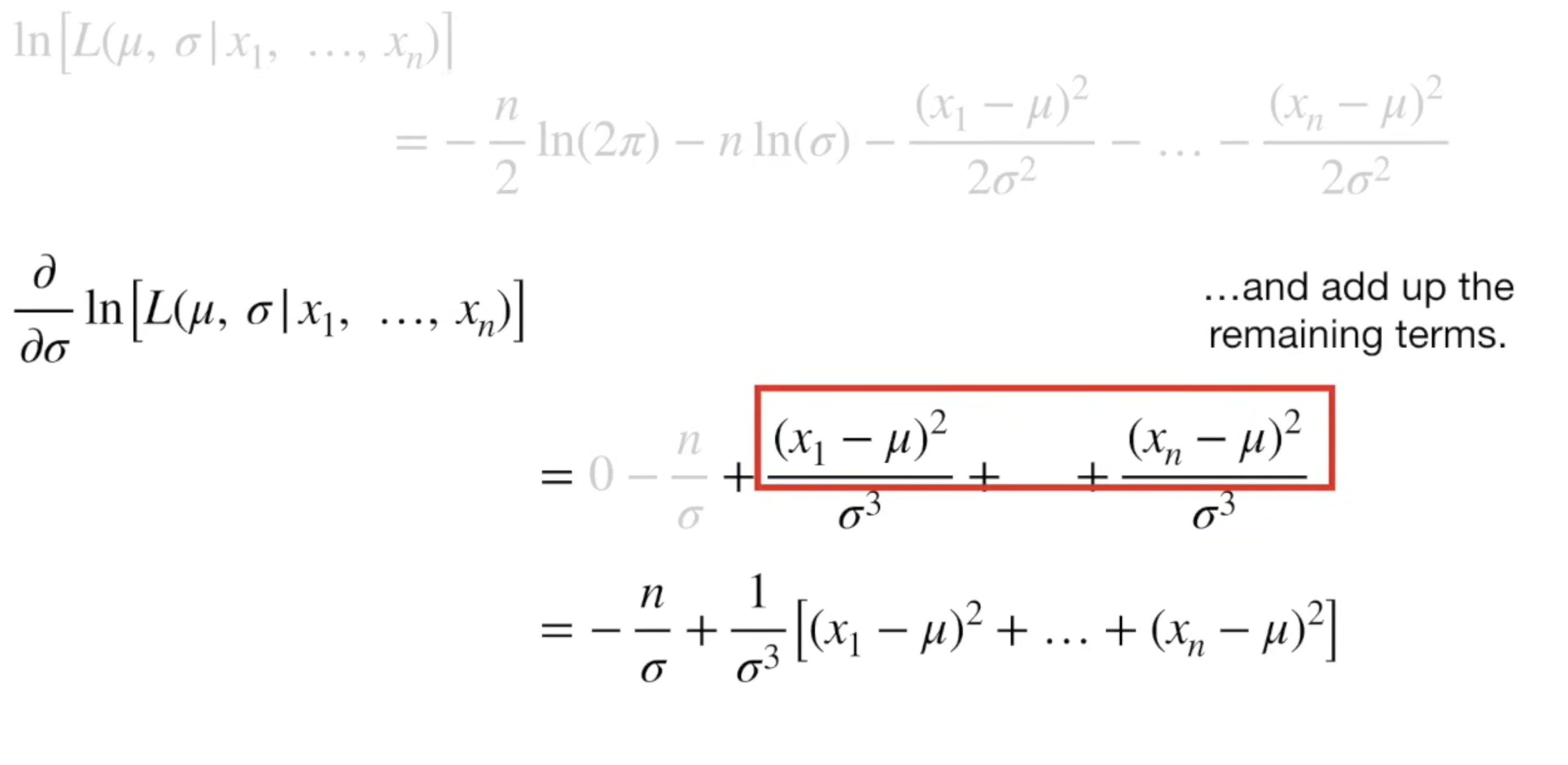 So the results is a well-known formula
So the results is a well-known formula
 Last not least, the probability vs likelyhood
Last not least, the probability vs likelyhood

2 Variational Auto Encoder
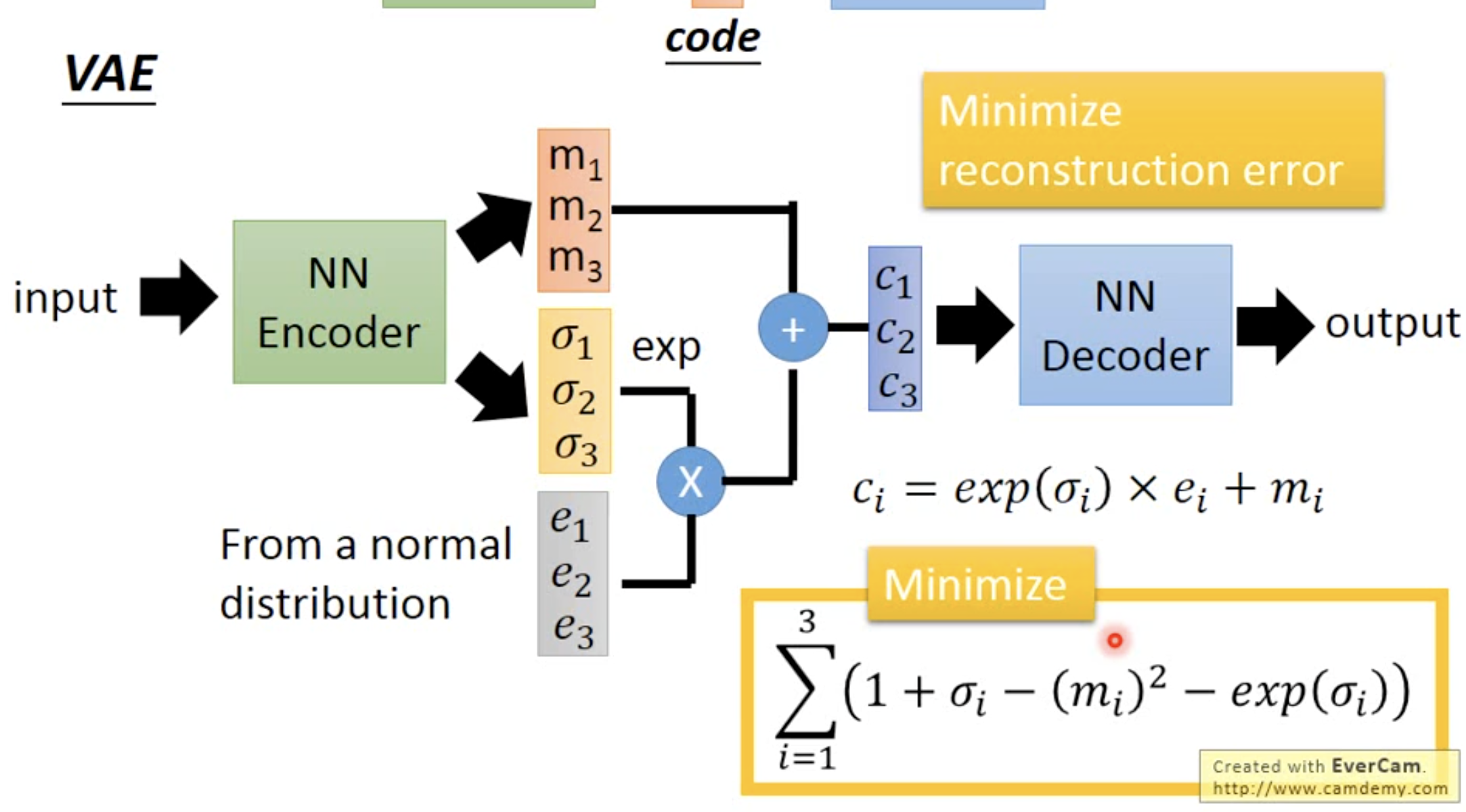
VAE is an AE, instead of encode to a embeded vector, it encode to a mean and a variance
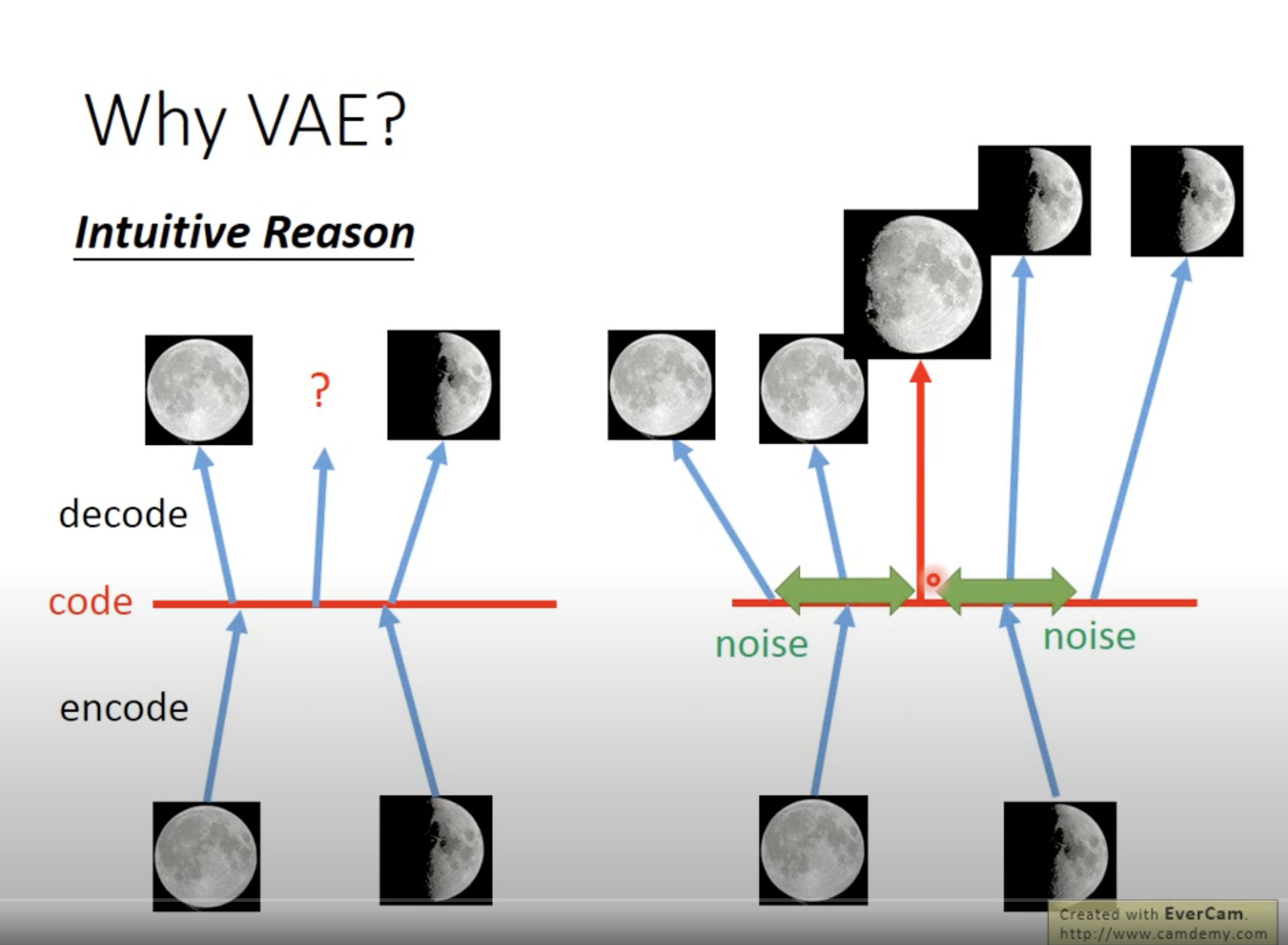
 The intuition is as following
The intuition is as following
- AE only maps to discreted points in the latent space, so the points in between may have NO meaning
- VAE is trying to map to points with noise, so all the points within the noise range can be decoded to the original image, with some variance
- So a point in between, should have features of all points around it, so it can generate a more meaningful picture
 The loss function of VAE has two parts, the first one is the constructional loss, same as AE.
The loss function of VAE has two parts, the first one is the constructional loss, same as AE.
The second part is essencially force the variance to be 1 instead of 0. Otherwise the best way to minimize loss is same as AE, which is have zero variance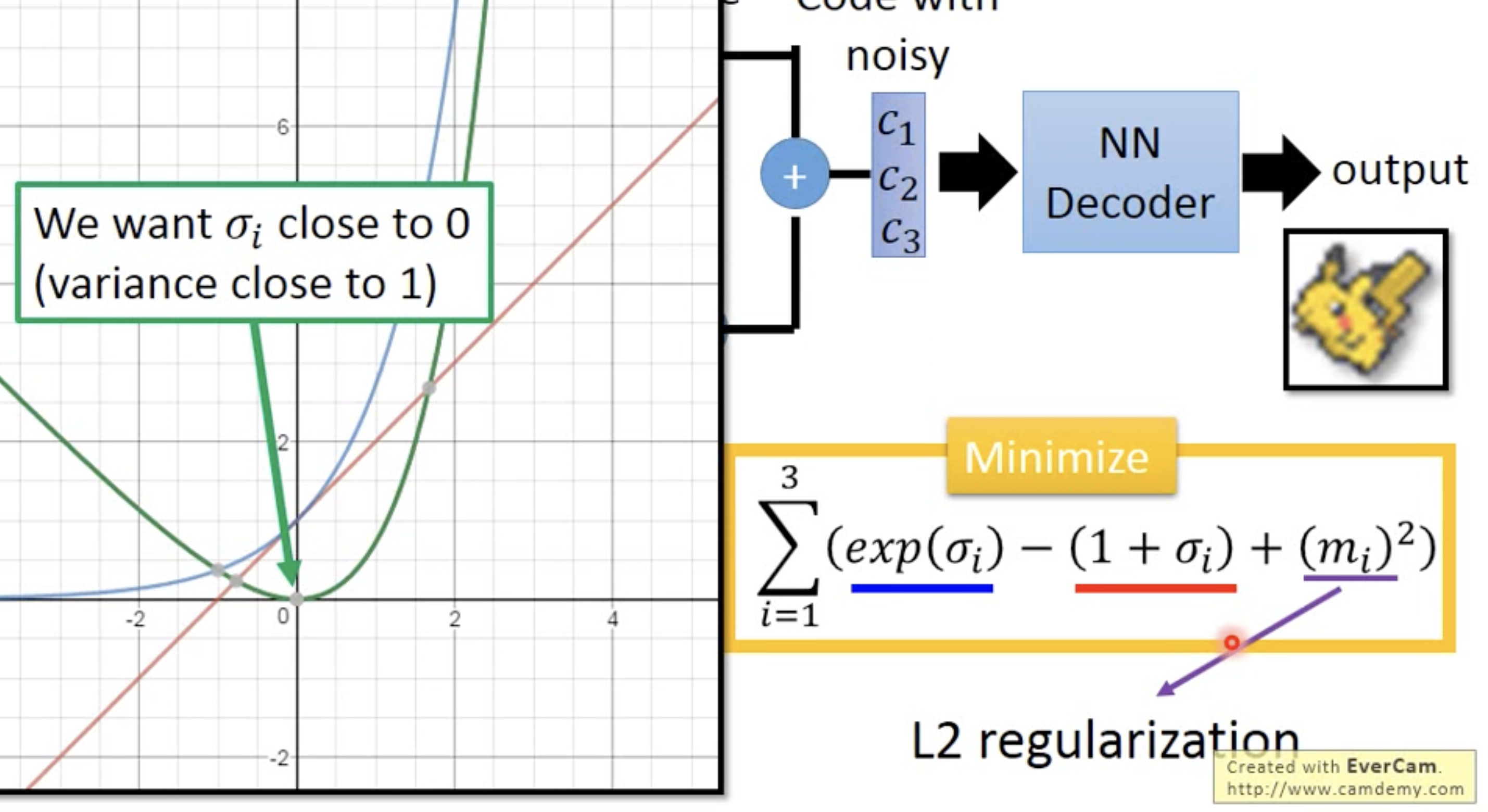
3 Some Math details
Any distribution can be expressed as Gaussian Mixture Model. The conditional prob $p(x|z)$ is a normal distribution with mean and var from a list of values.
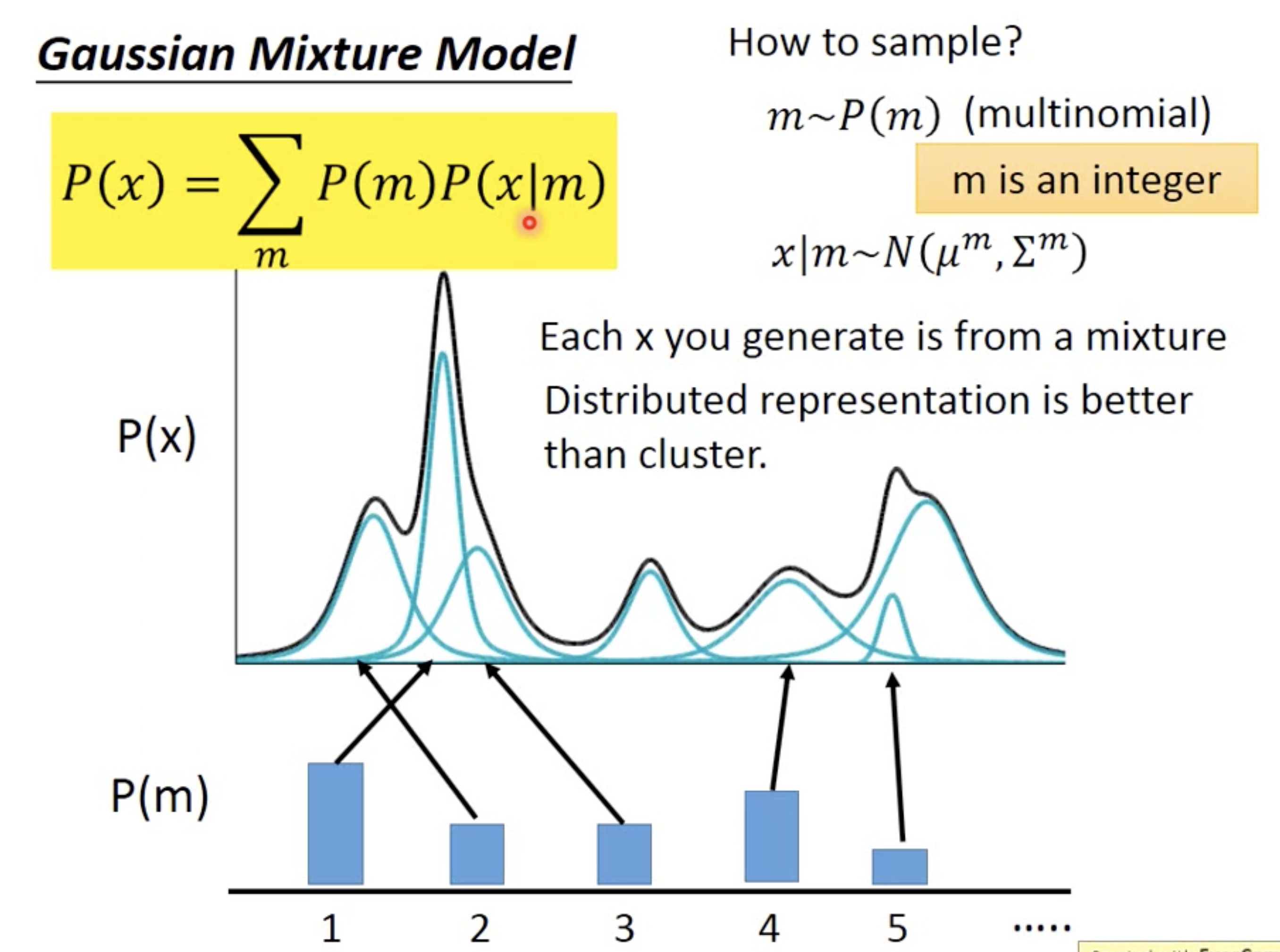 Instead of using m discreted clusters, we can use continuous normal distribution z. and $p(x|z)$ is also a norm distribution with mean and variance generated by a NN (encoder)
Instead of using m discreted clusters, we can use continuous normal distribution z. and $p(x|z)$ is also a norm distribution with mean and variance generated by a NN (encoder)
 In order to estimate the mean and var, we would like to maximize the likelihoof of observed data, so it’s MLE
In order to estimate the mean and var, we would like to maximize the likelihoof of observed data, so it’s MLE
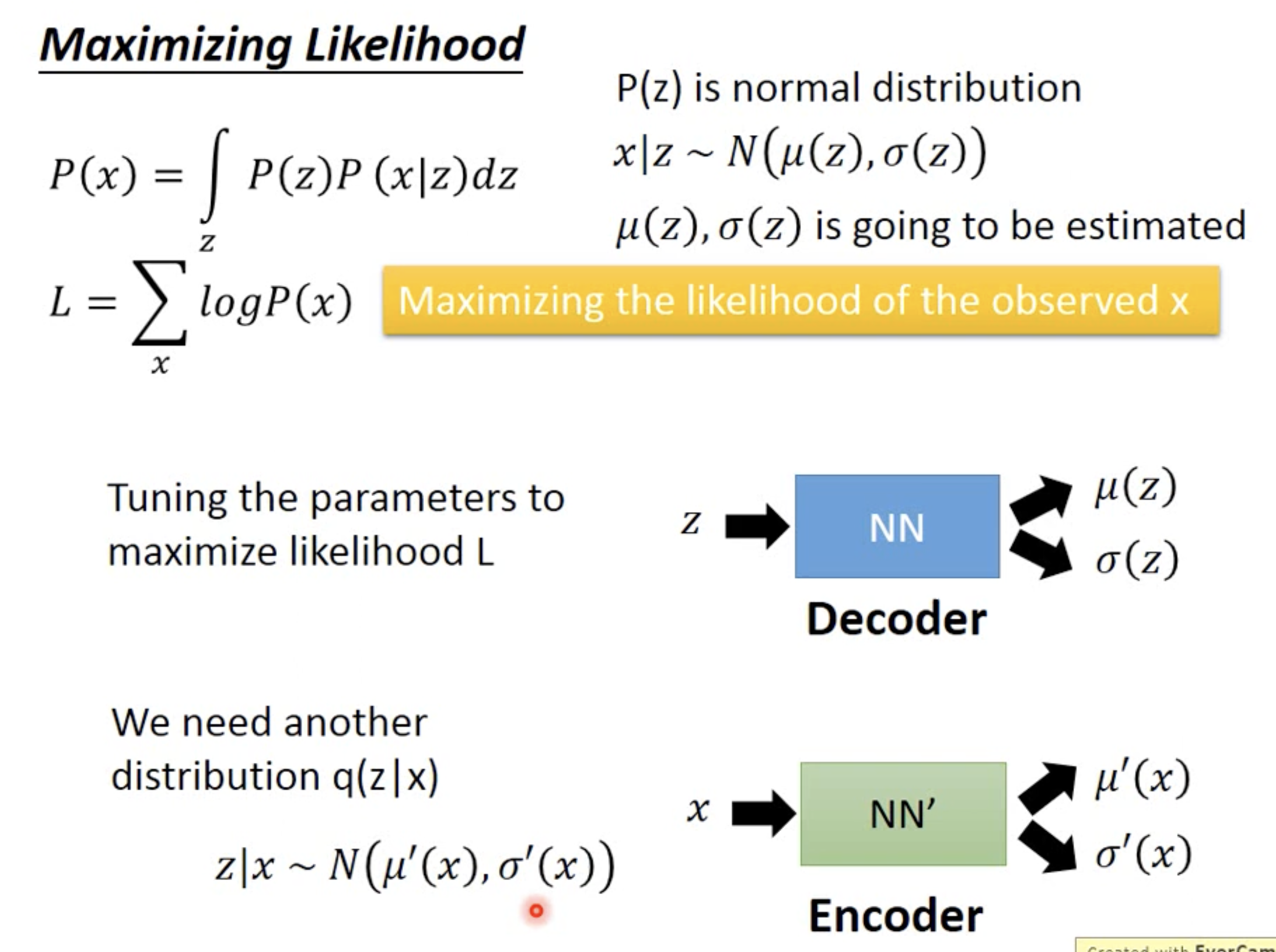 The introduced $q(z|x)$ is actually our encoder. We can rewrite the likehood formula with q giving that the integral over z is always 1
The introduced $q(z|x)$ is actually our encoder. We can rewrite the likehood formula with q giving that the integral over z is always 1
 After some math, the problem becomes we need to increase the lowber bound.
But increase the lower bound does NOT garantee increase the likelihood, unless we minimized the KL between p and q, which make our likelihood more close to the lower bound
After some math, the problem becomes we need to increase the lowber bound.
But increase the lower bound does NOT garantee increase the likelihood, unless we minimized the KL between p and q, which make our likelihood more close to the lower bound
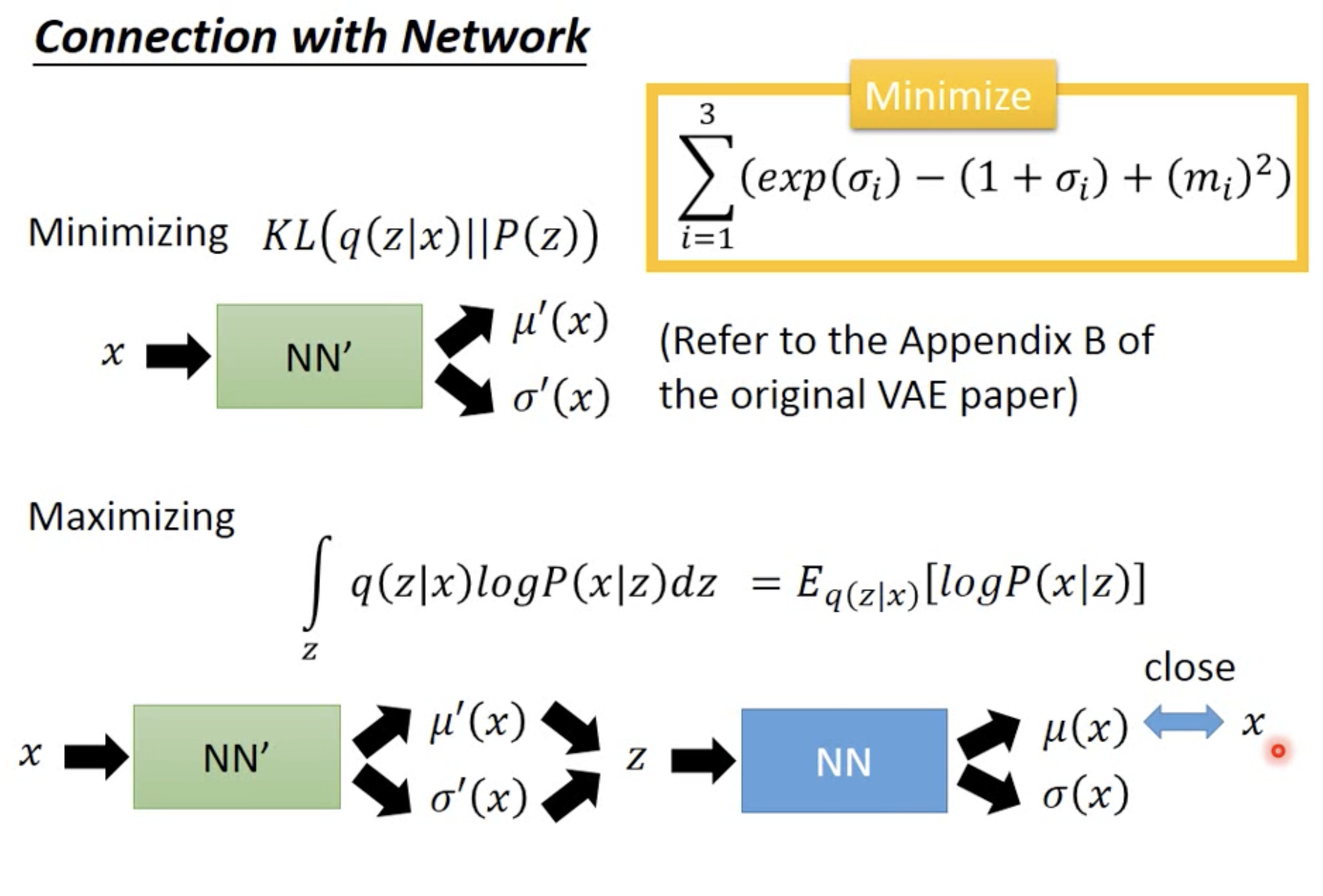
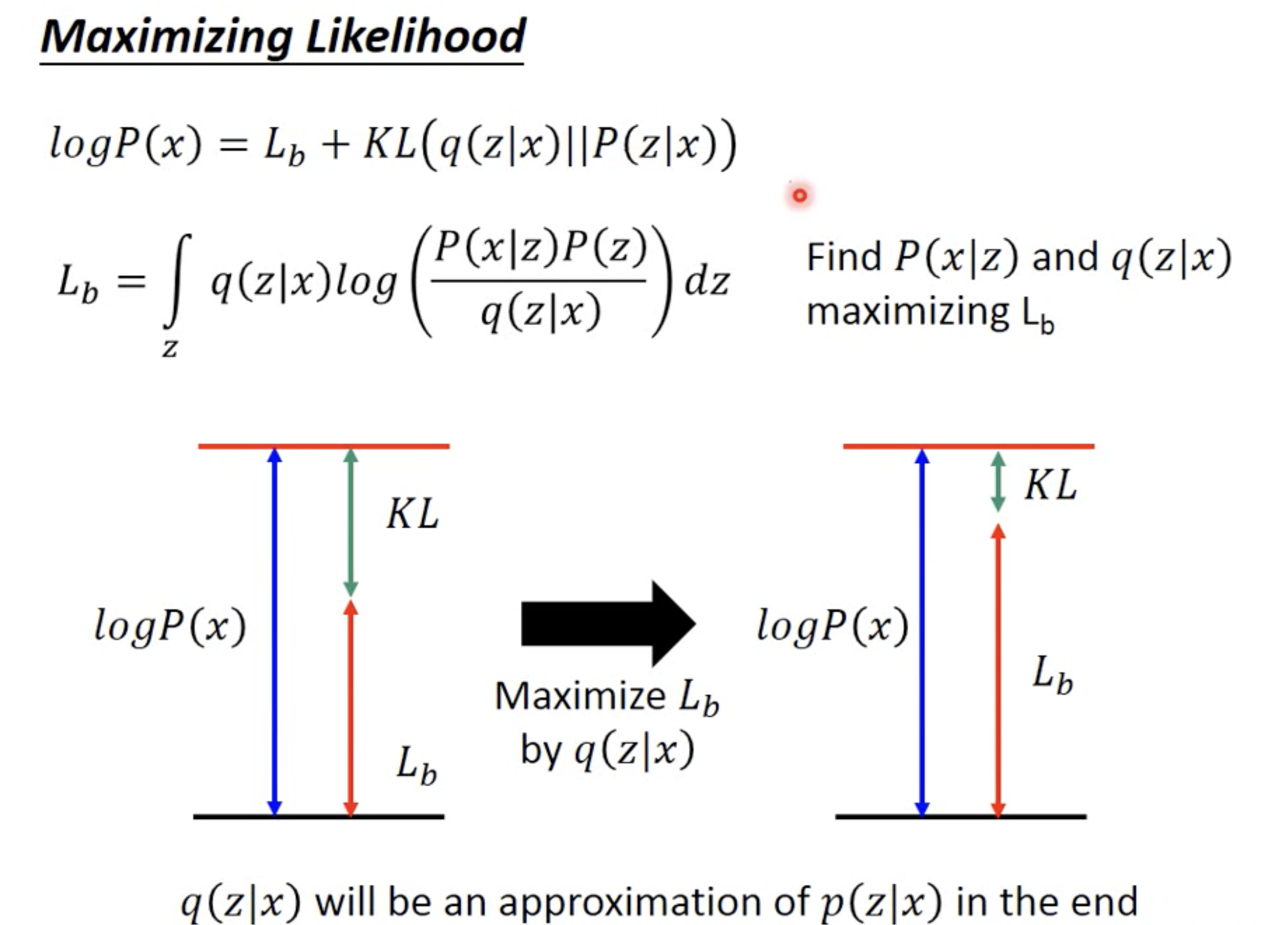 Now let’s break down the lower bound
Now let’s break down the lower bound
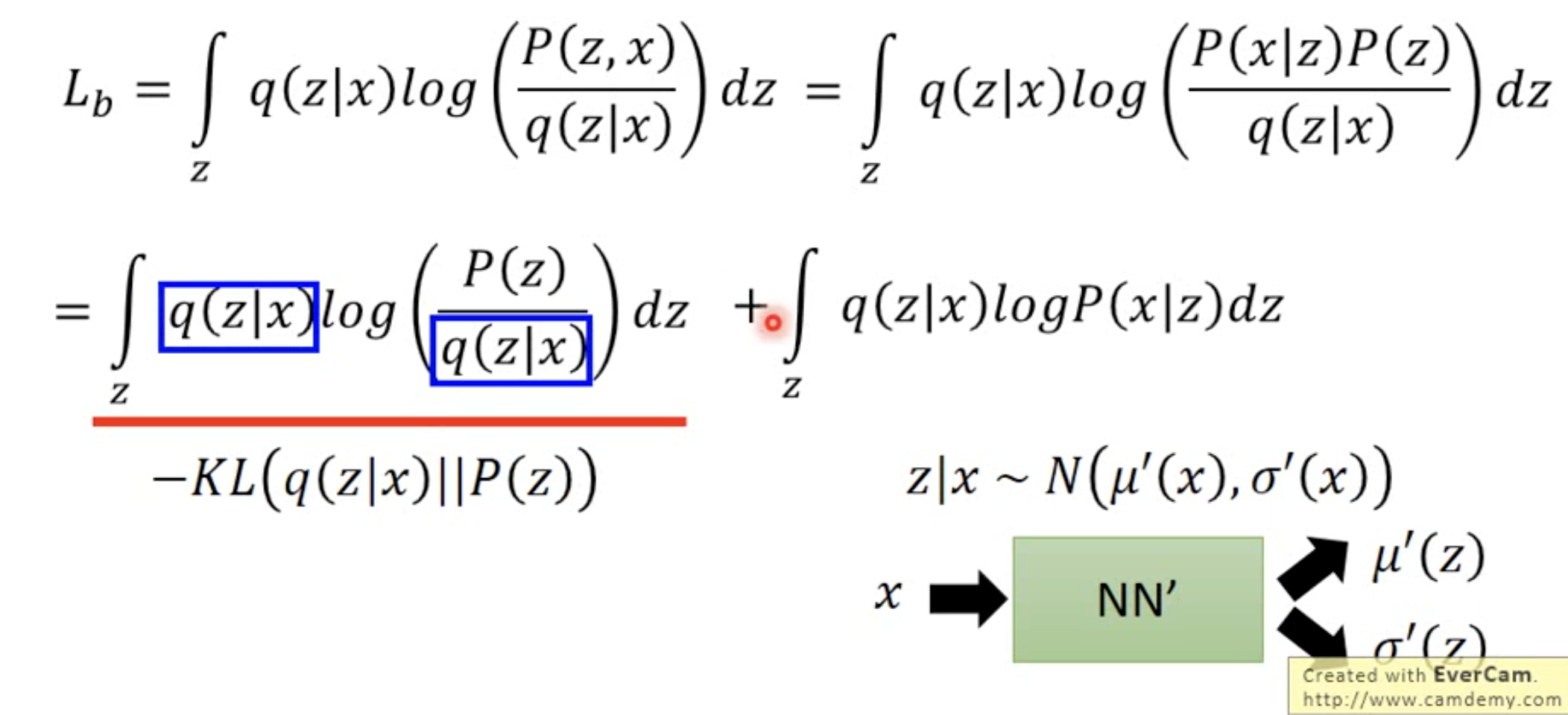 So it has two parts of this LB
So it has two parts of this LB
-
Making the $q(z x)$ normal, which is more close to norm distribution of p(z) - Maximize the second part, which is essencially make the output close to sampled x, which is the construction loss part
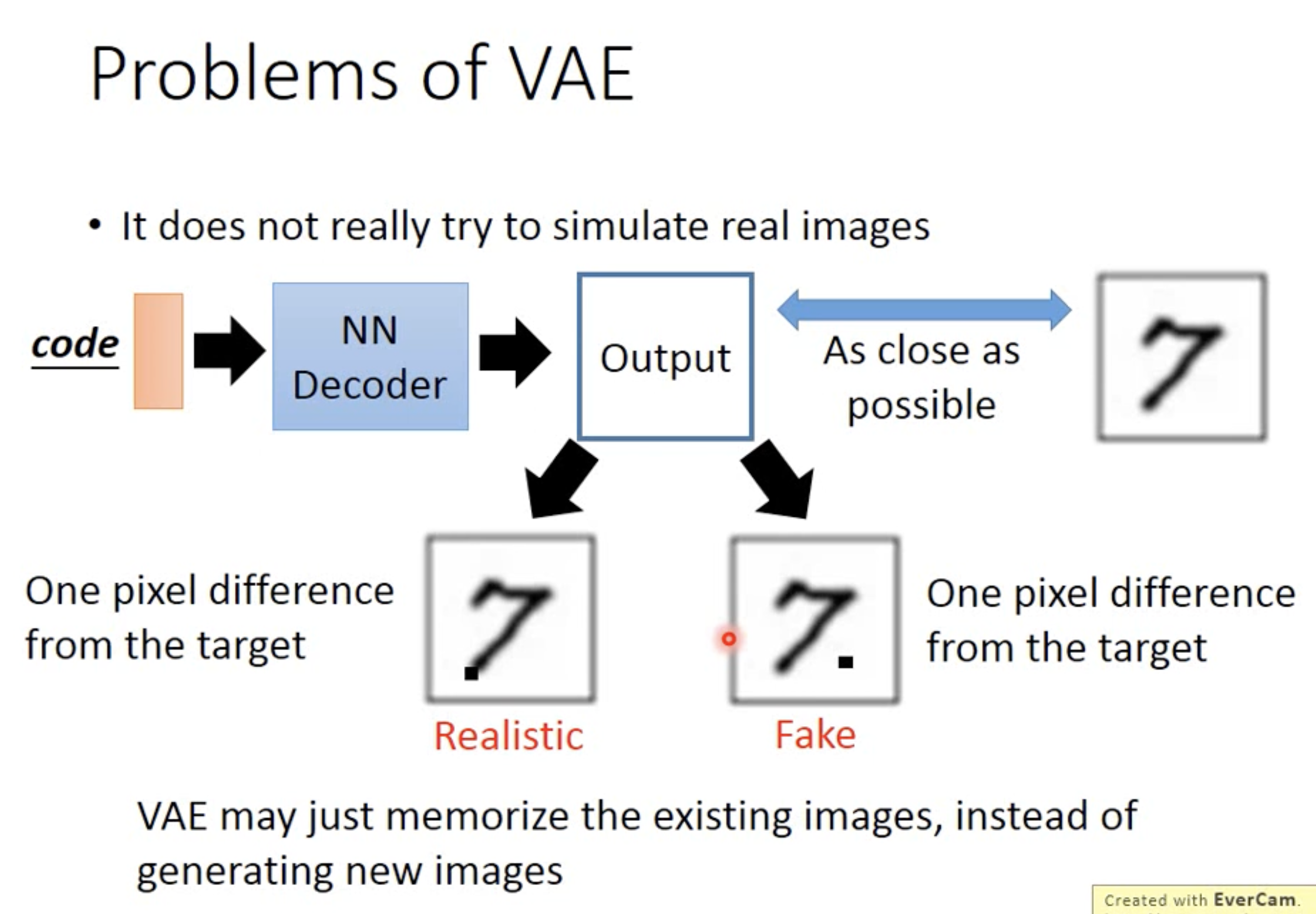
4 Problem of VAE
The main issue of VAE is that it only trys to synthesis from sample images, but never really try to generate new ones. The solution to this problem is using GAN, which adds a discriminator for better generating purpose
 A bit sad that I never took any notes when I learnt GAN, which is the coolest thing since the invention of “sliced bread”, according to LeCun. GAN is a bit of outdate these days, so I don’t think I will review it any time soon. But that’s where I firstly learned KL Divergence, thanks to Ian and his GAN paper.
A bit sad that I never took any notes when I learnt GAN, which is the coolest thing since the invention of “sliced bread”, according to LeCun. GAN is a bit of outdate these days, so I don’t think I will review it any time soon. But that’s where I firstly learned KL Divergence, thanks to Ian and his GAN paper.