Quantum Computing

I knew that Quantum Computing is NOT about parallelism but never truely understand how it works. Thanks for 3Blue1Brown’s great explanation video here, I finally get a idea of the basics

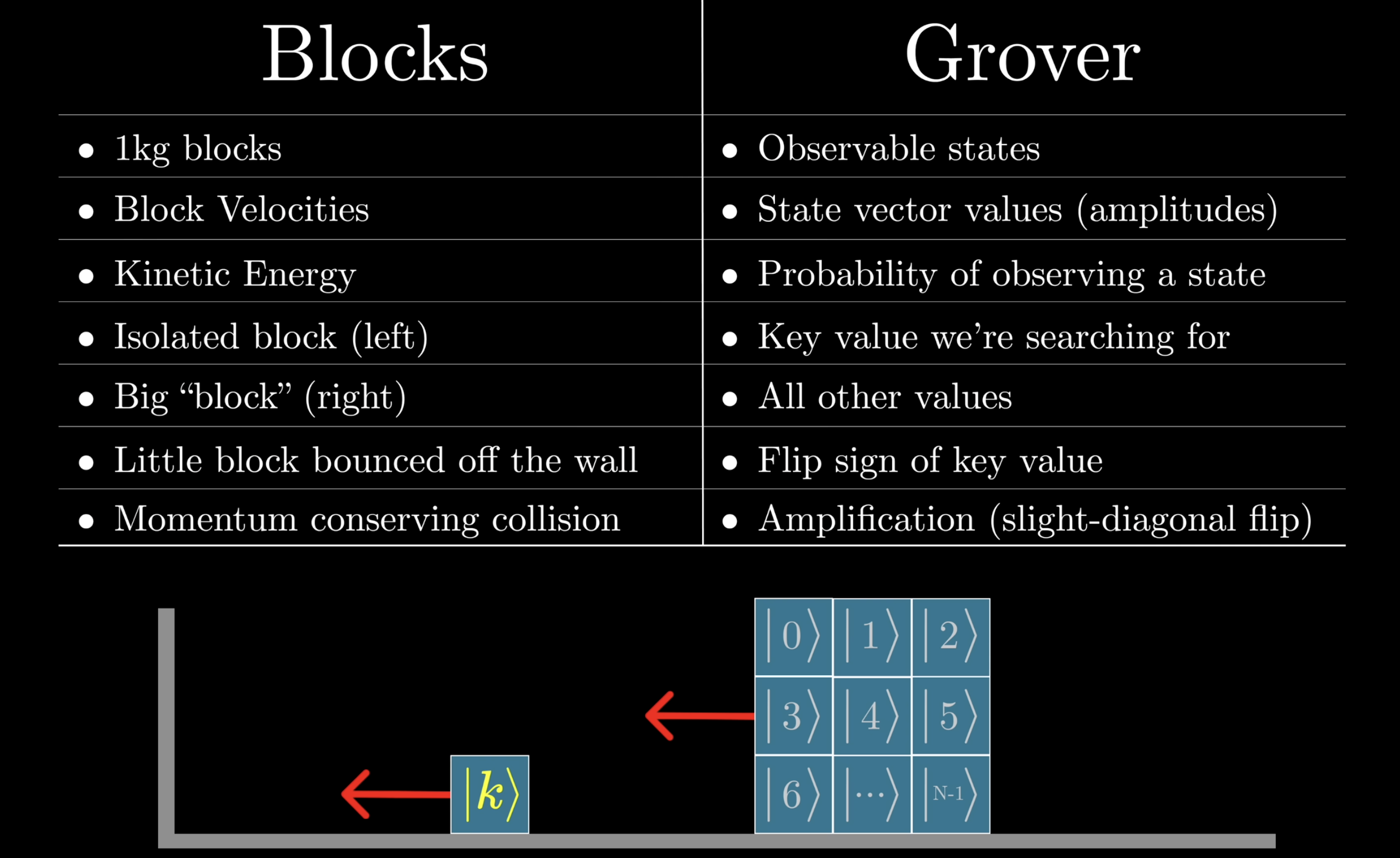
It starts with a simple question, there are N numbers and how to find a unique number that makes f(x)=1 while all others f(x)=0

1 Quant

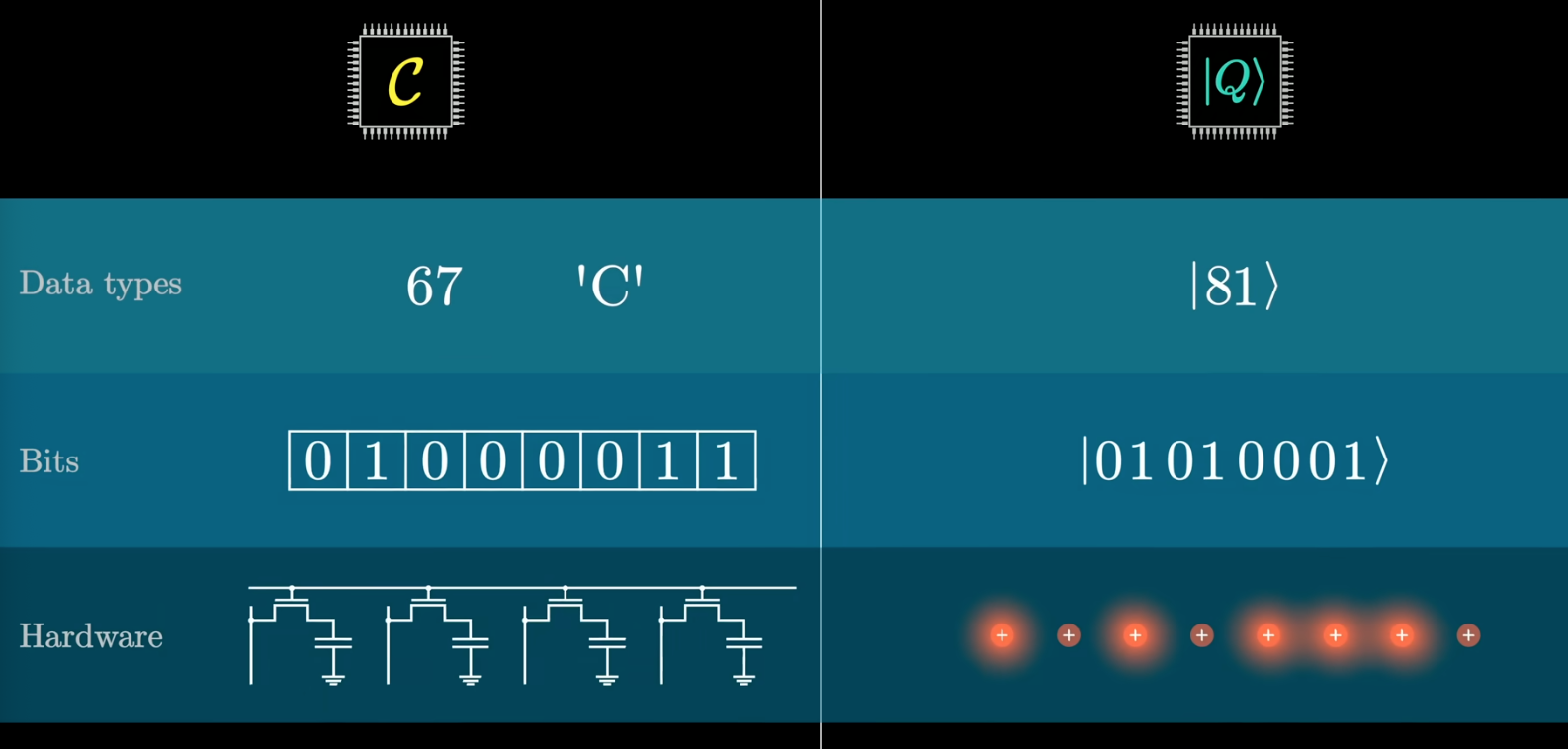
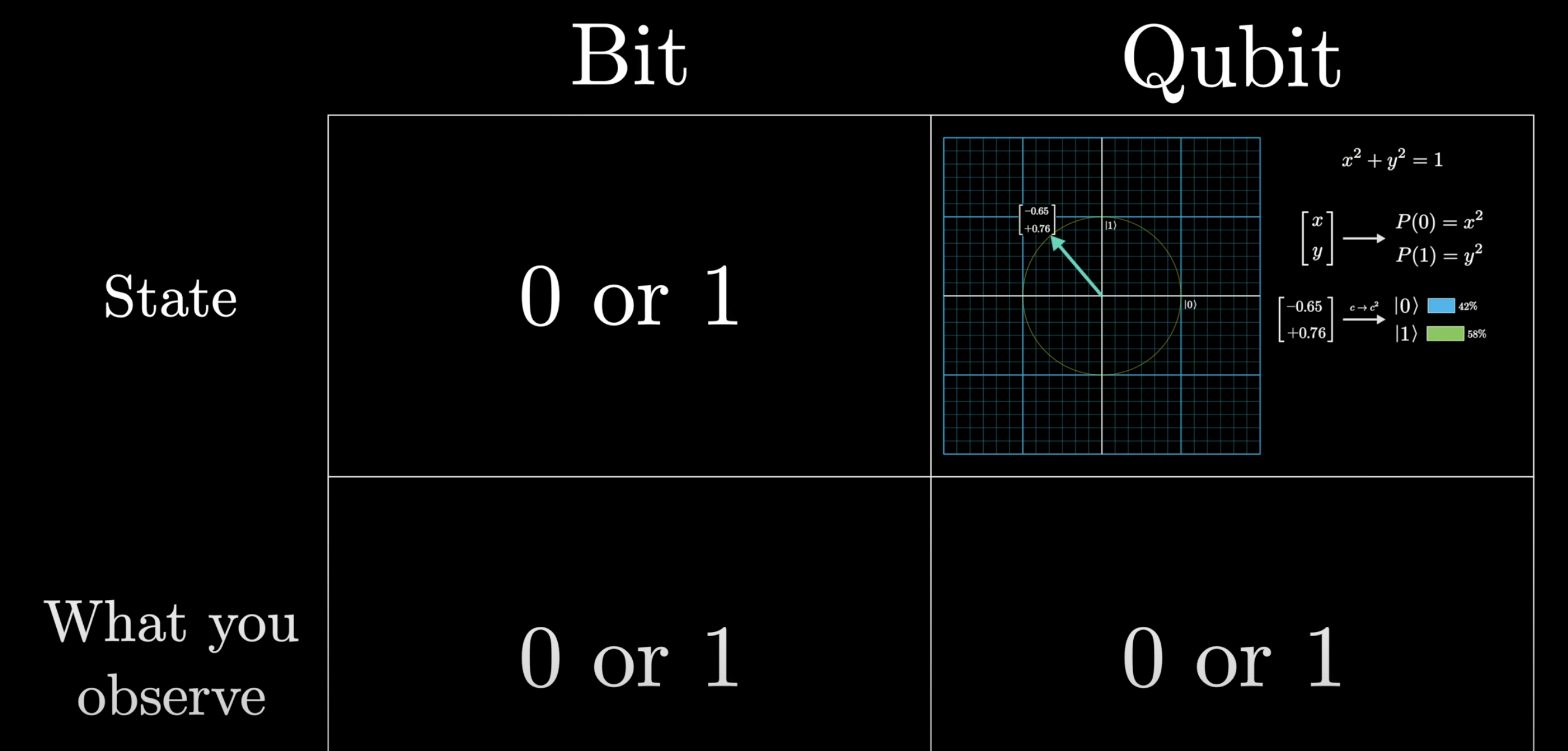
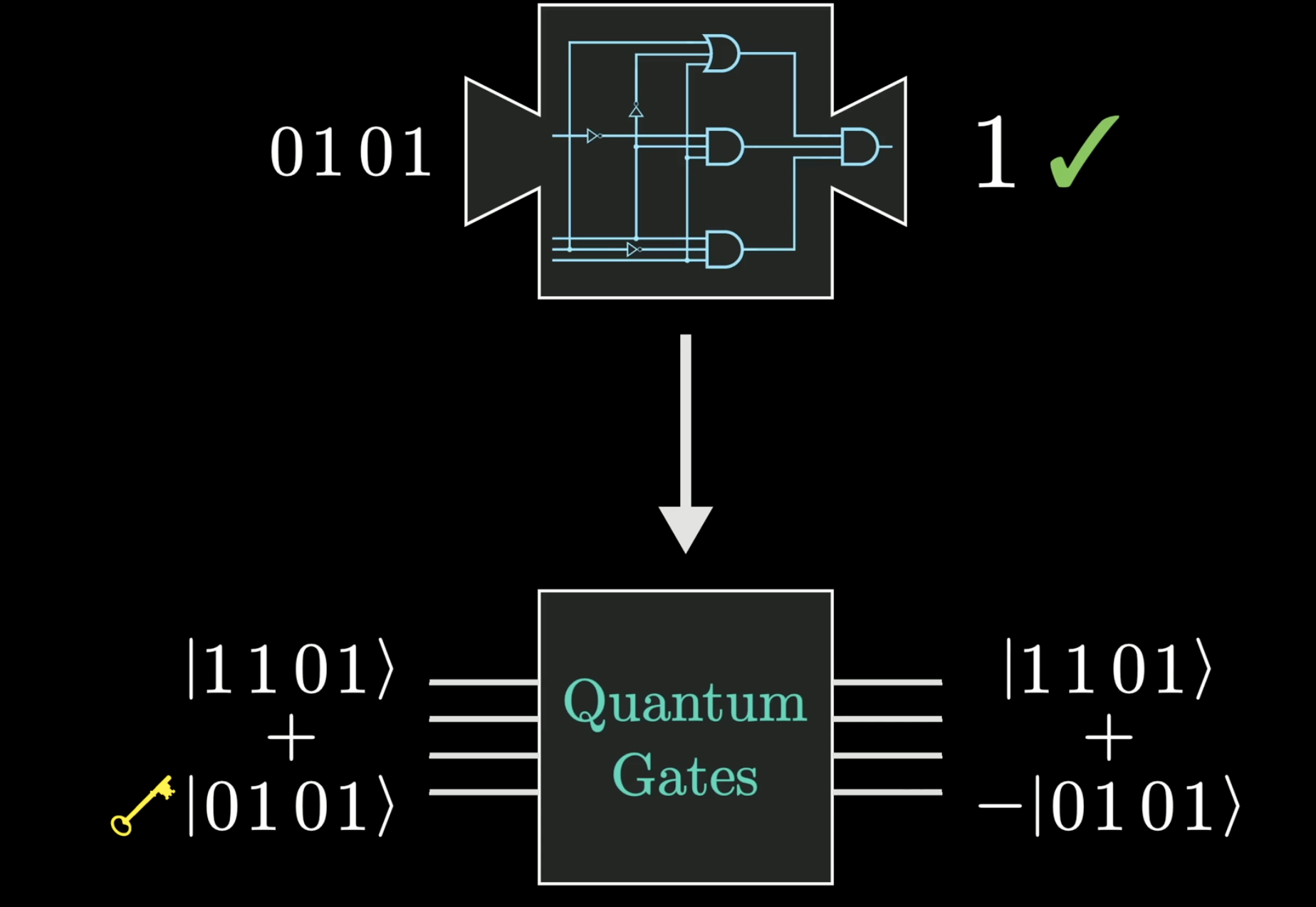
It starts with comparing with classic computer, where we get bits out of the hardware and translate them into numbers of digits

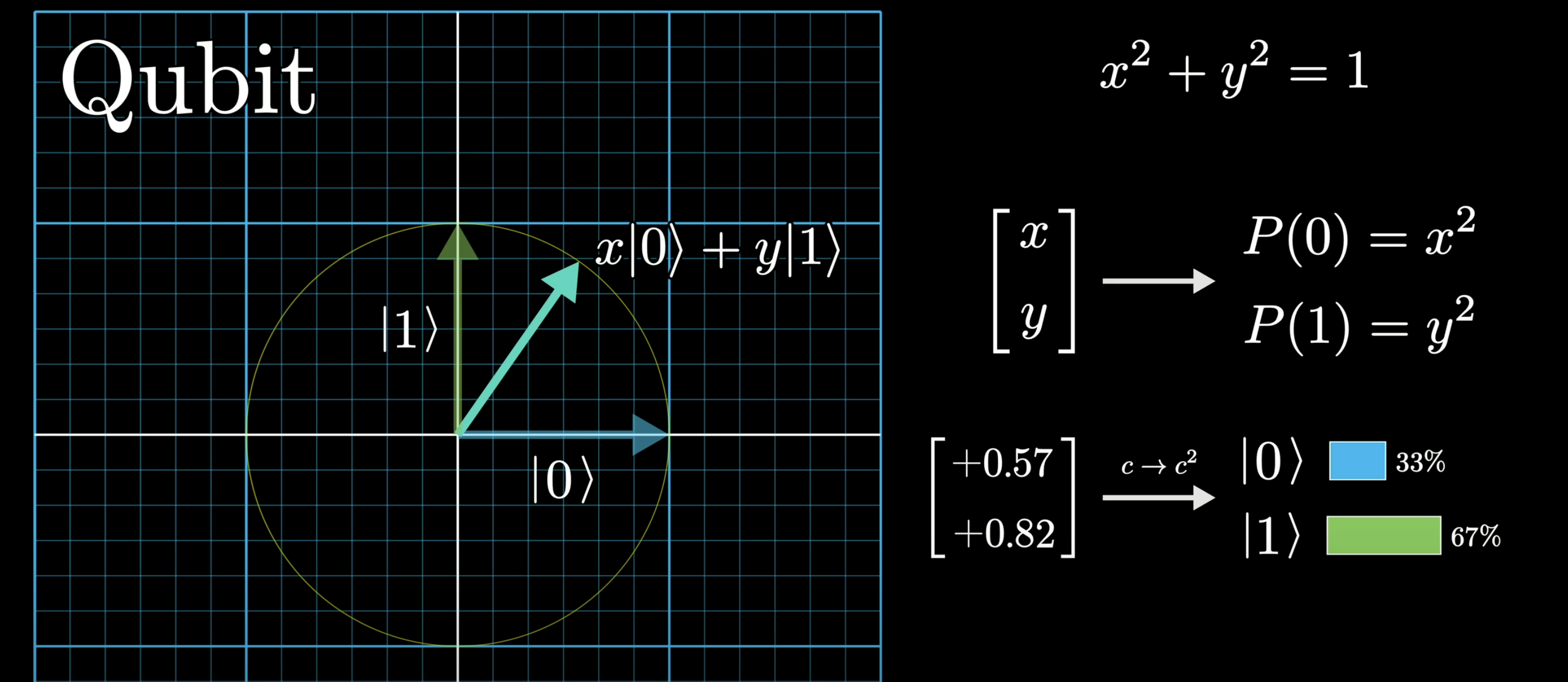
Quantum computer uses qubits(number put in ket), and a number is sampled from the quantum hardware

The state read from quantum memory is NOT always the same, but a random number. But after you read it once, the number will be fixed in the later read. 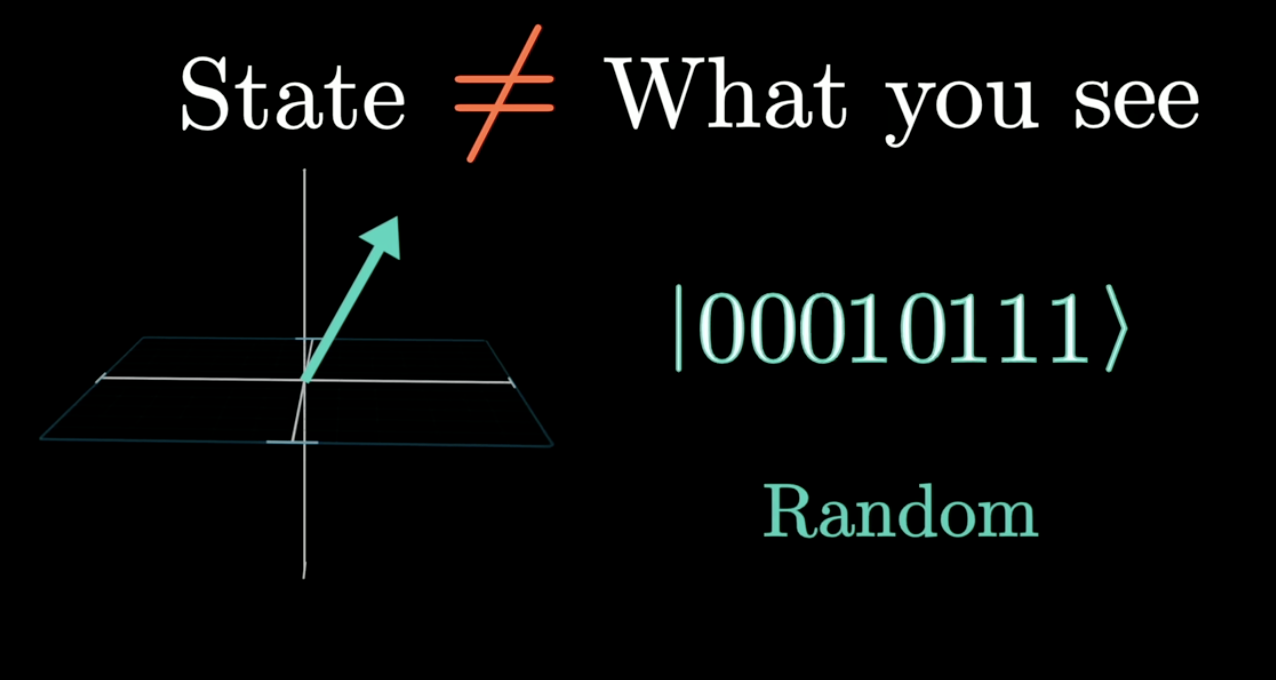So the state vectors are used to calculate the probability of reading a number out of the memory

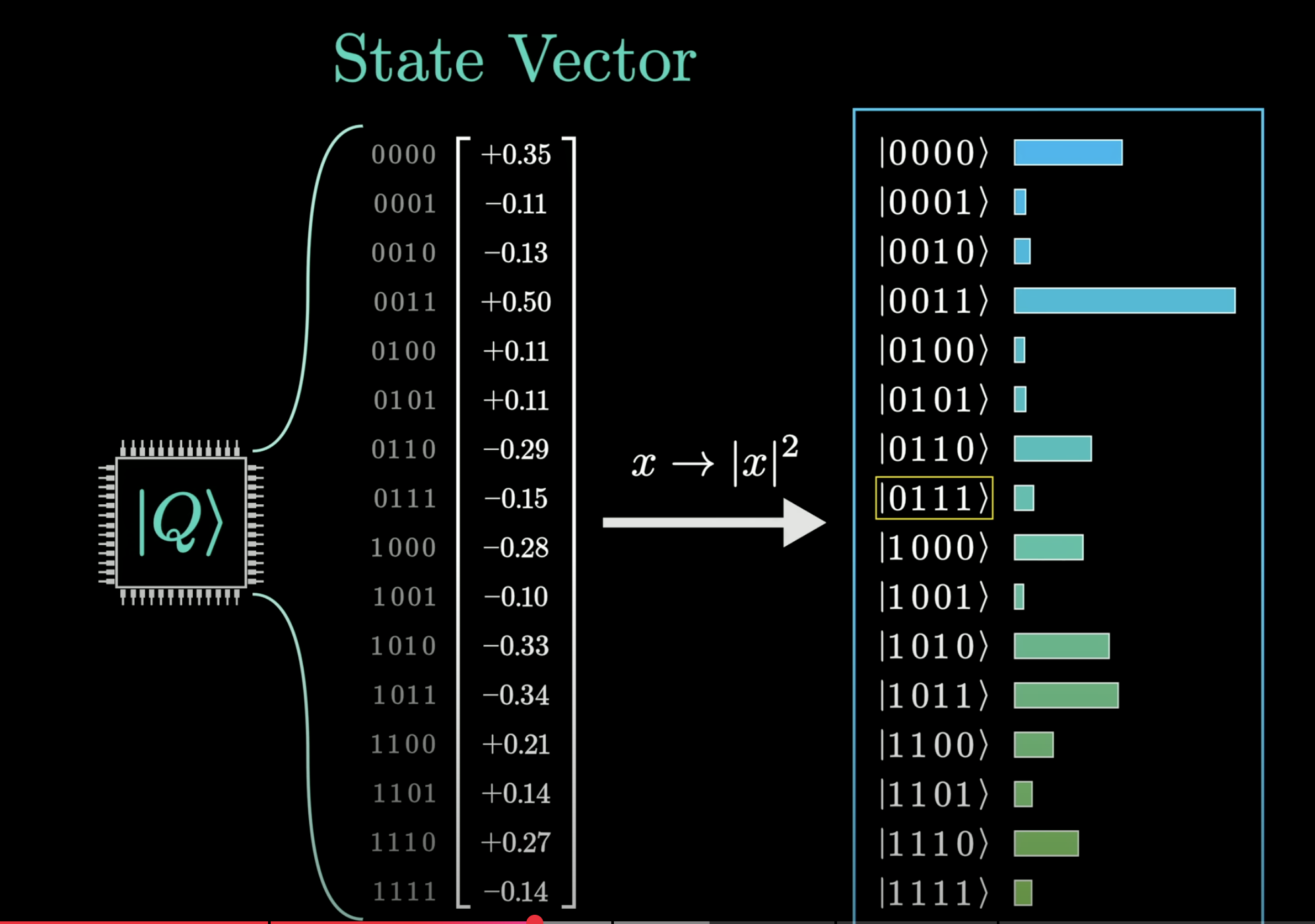
State vectors can be considered as the coordinates of a high dim space. Use 2D as example you will see each state is a point on a circle Comparing to bits

2 Ket and quantum gates

The symbal ket means a unit vector in a state space, and we can represent any vector with combination of ket values

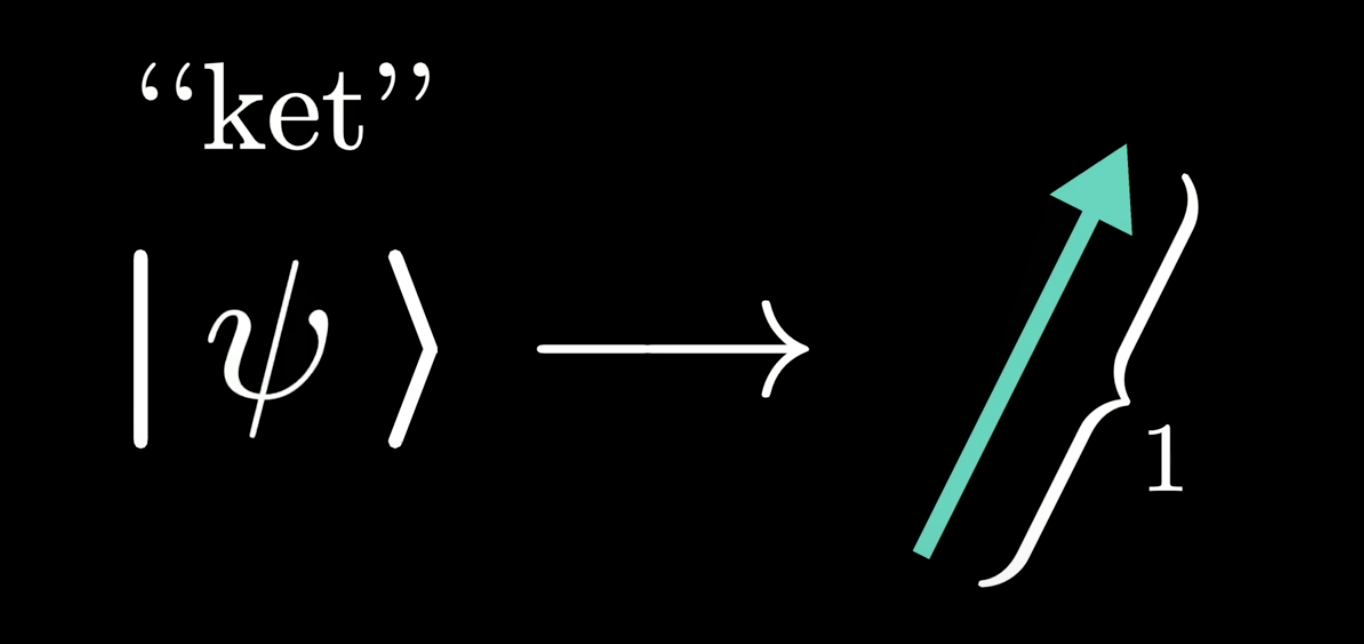
A quantum gates can manipulate these state vectors. One example is a gate called “”

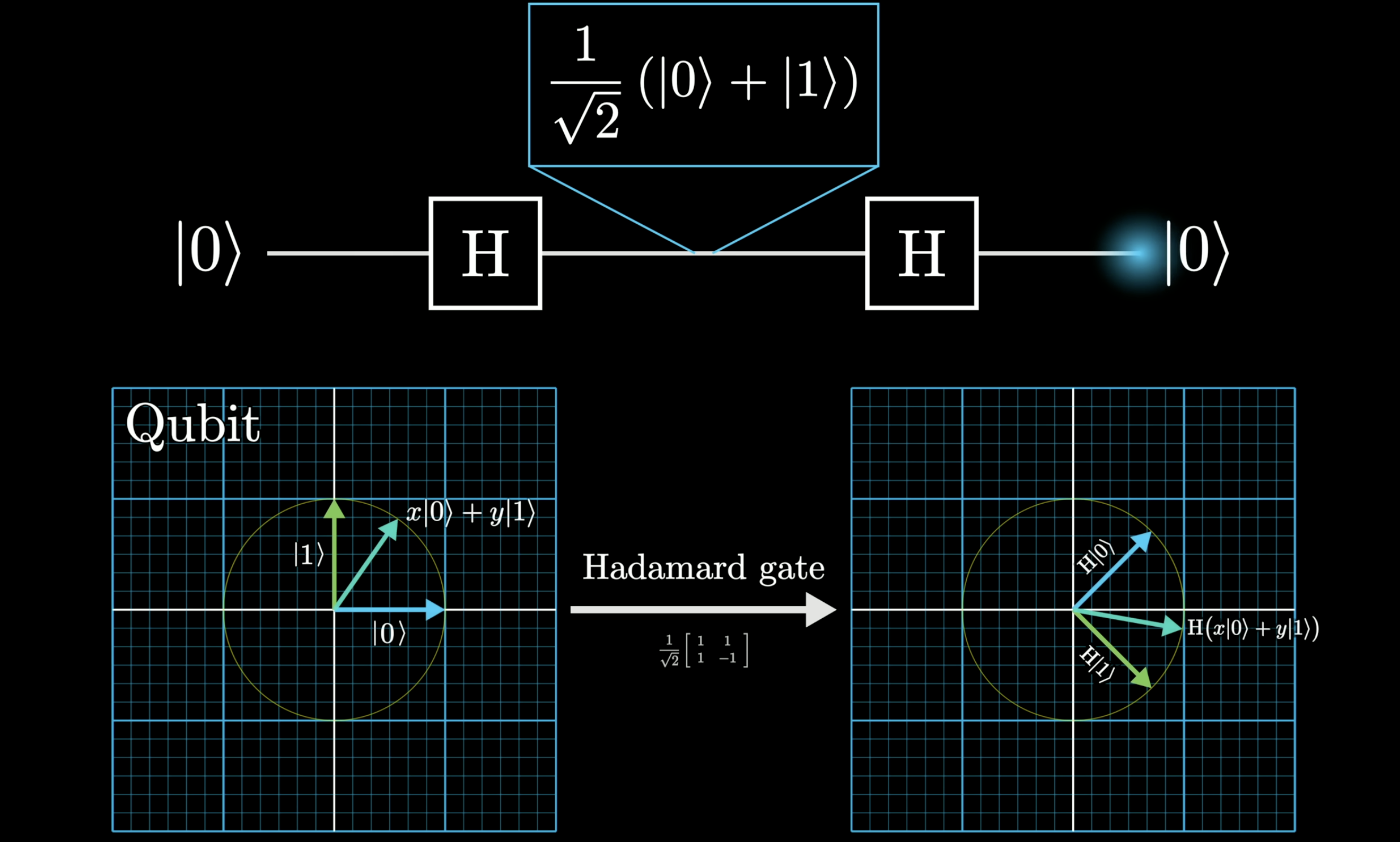
3 Grover’s Algorithem

A quantum algorithm is to manipulate state vectors, so that a desired state can have high probability that is the correct answer.

For a NP problem, which is hard to find answers but easy to verify, we can assume we have a logical gate which verify the answer. and a quantum gate can always be built based on this logical gates, and the output is the flipped signed state vector

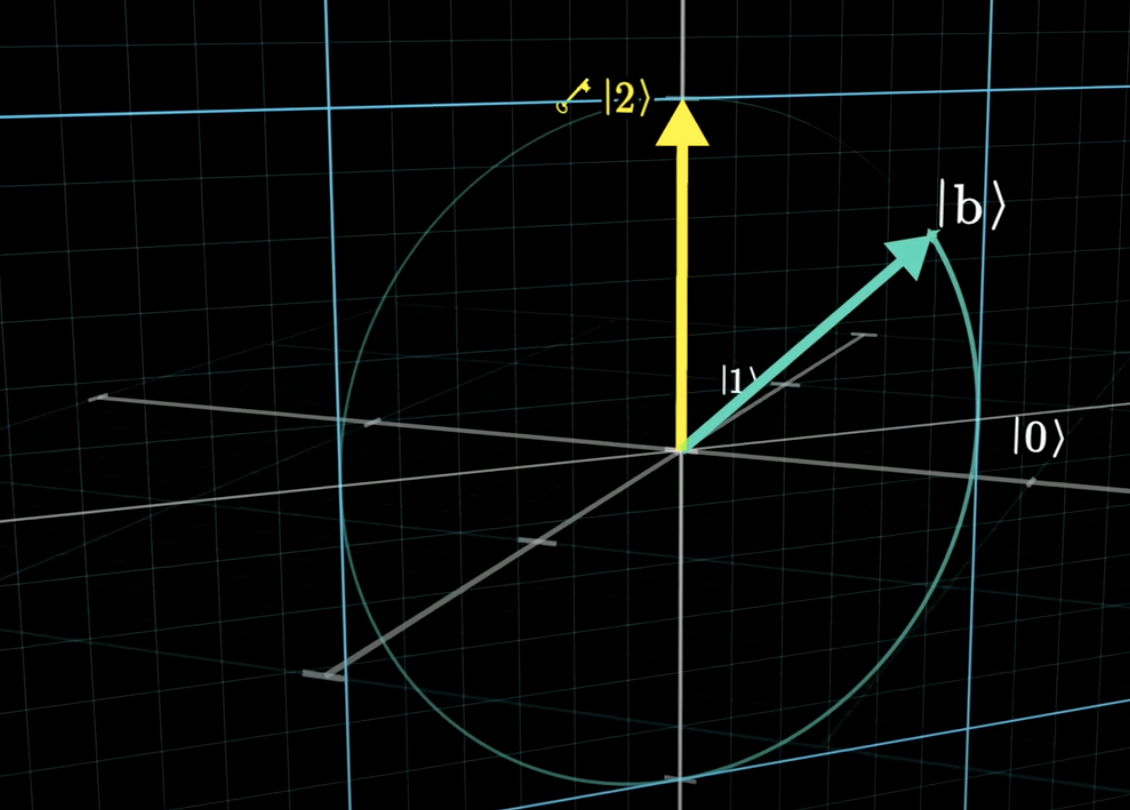
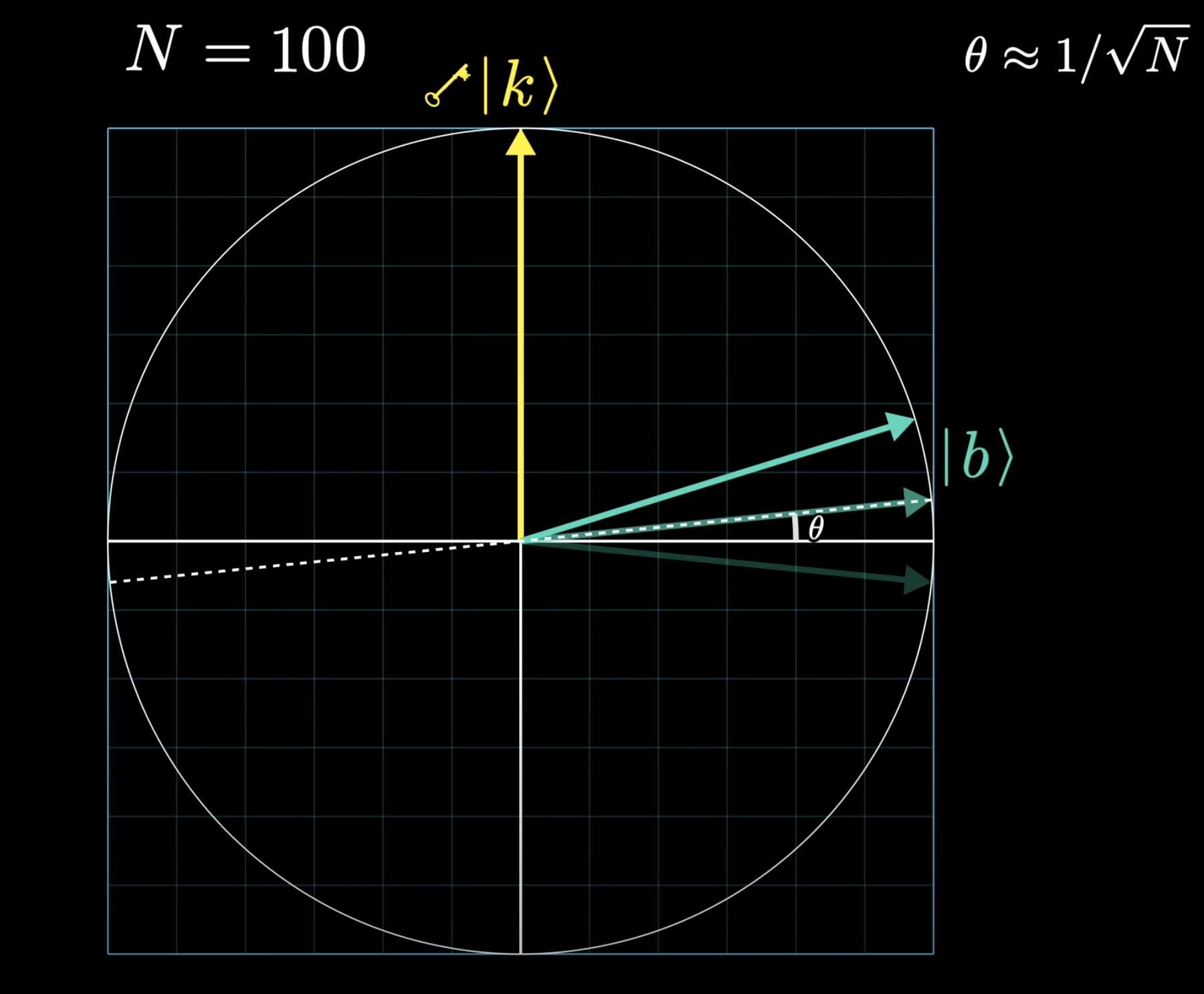
It starts with a balanced state, which is average of all unit vectors of a state space, and our goal is to move the vector to the answer vector.

We can only focus on the 2D plane which is the balanced vector and answer vector. The length of the vector can be calulcated as following and the angle is very important to understand the speedup from quantum

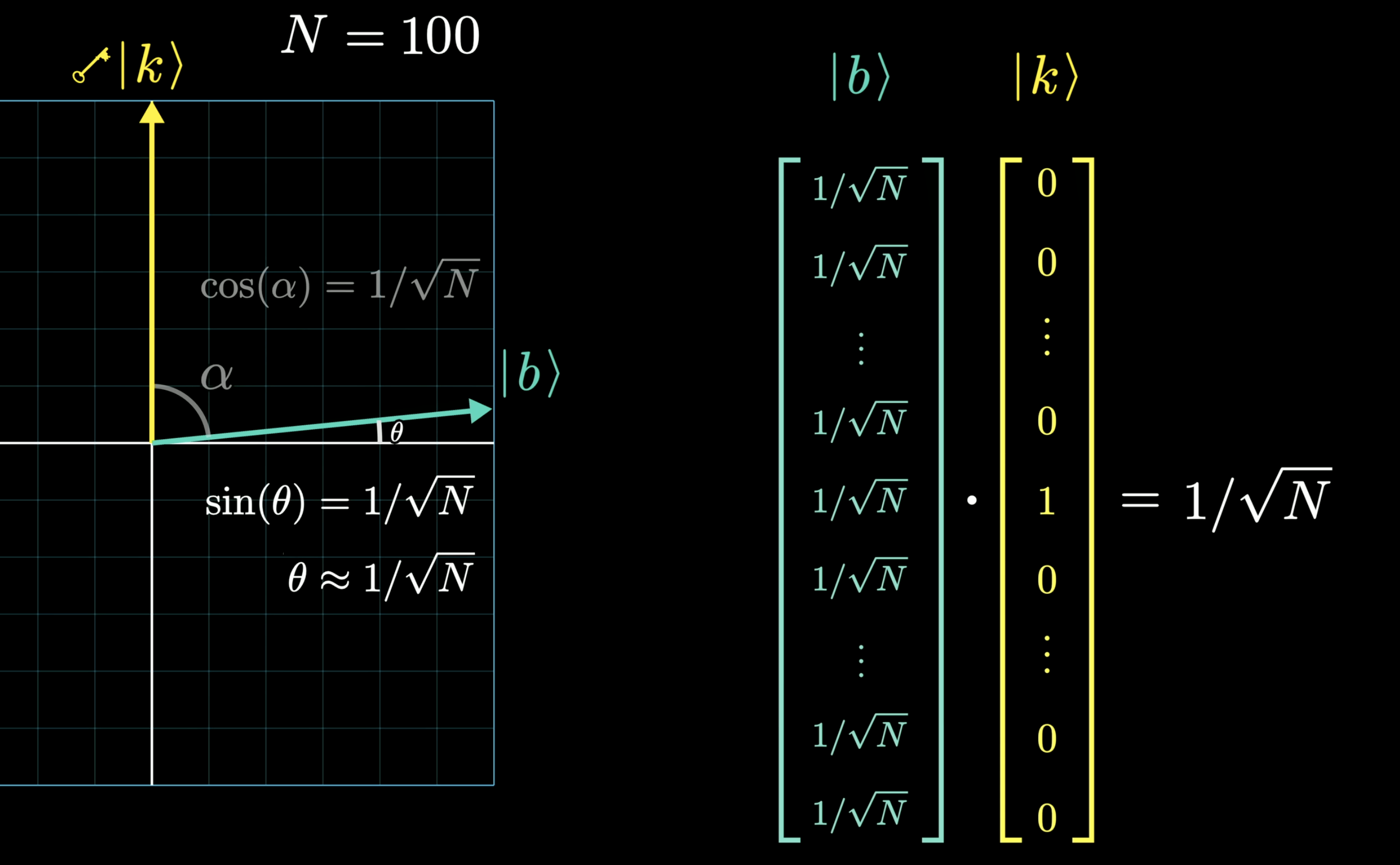
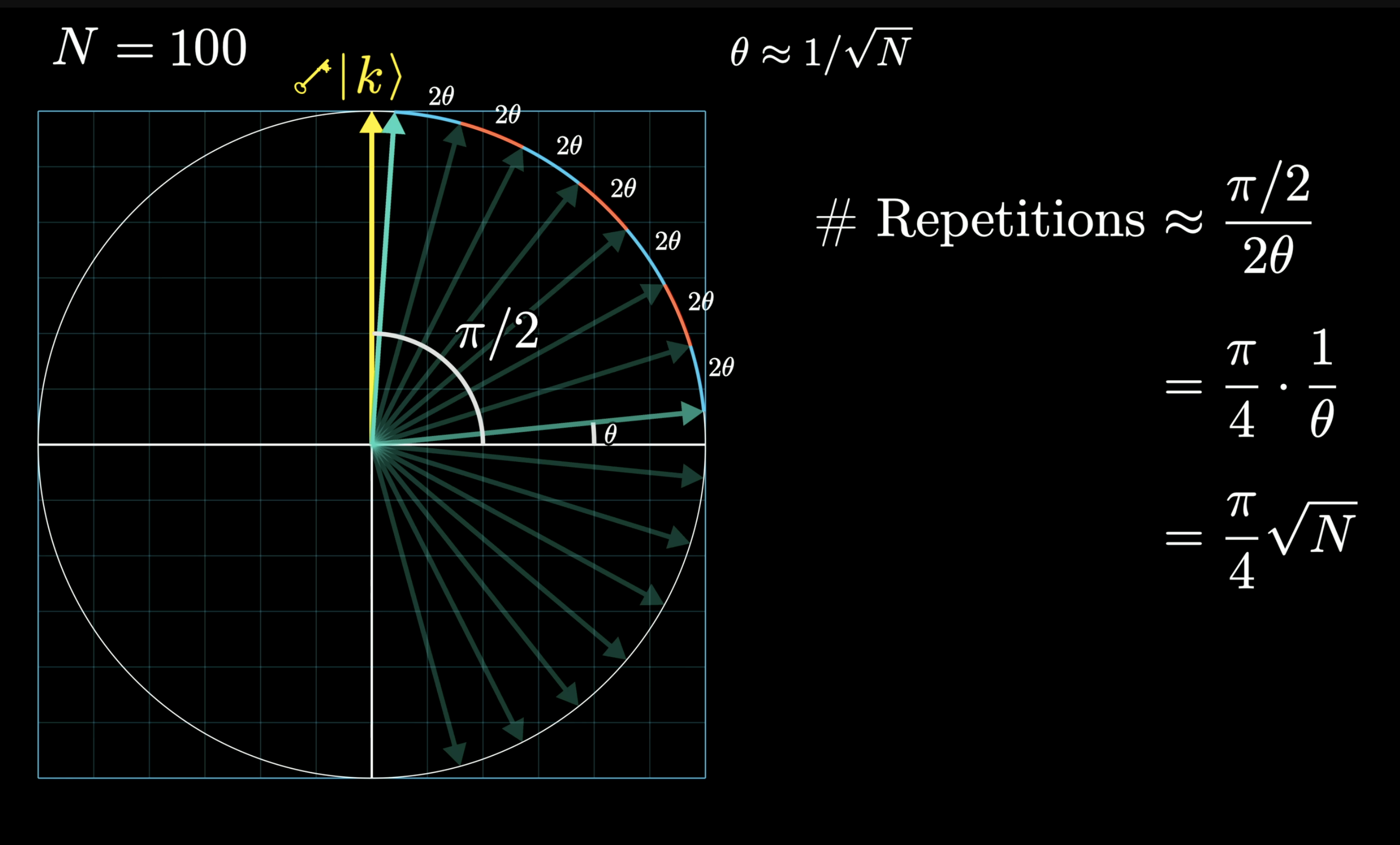
Now here are the steps of the algorithem

1. use the quantum gate the flip the balanced vector around X axis
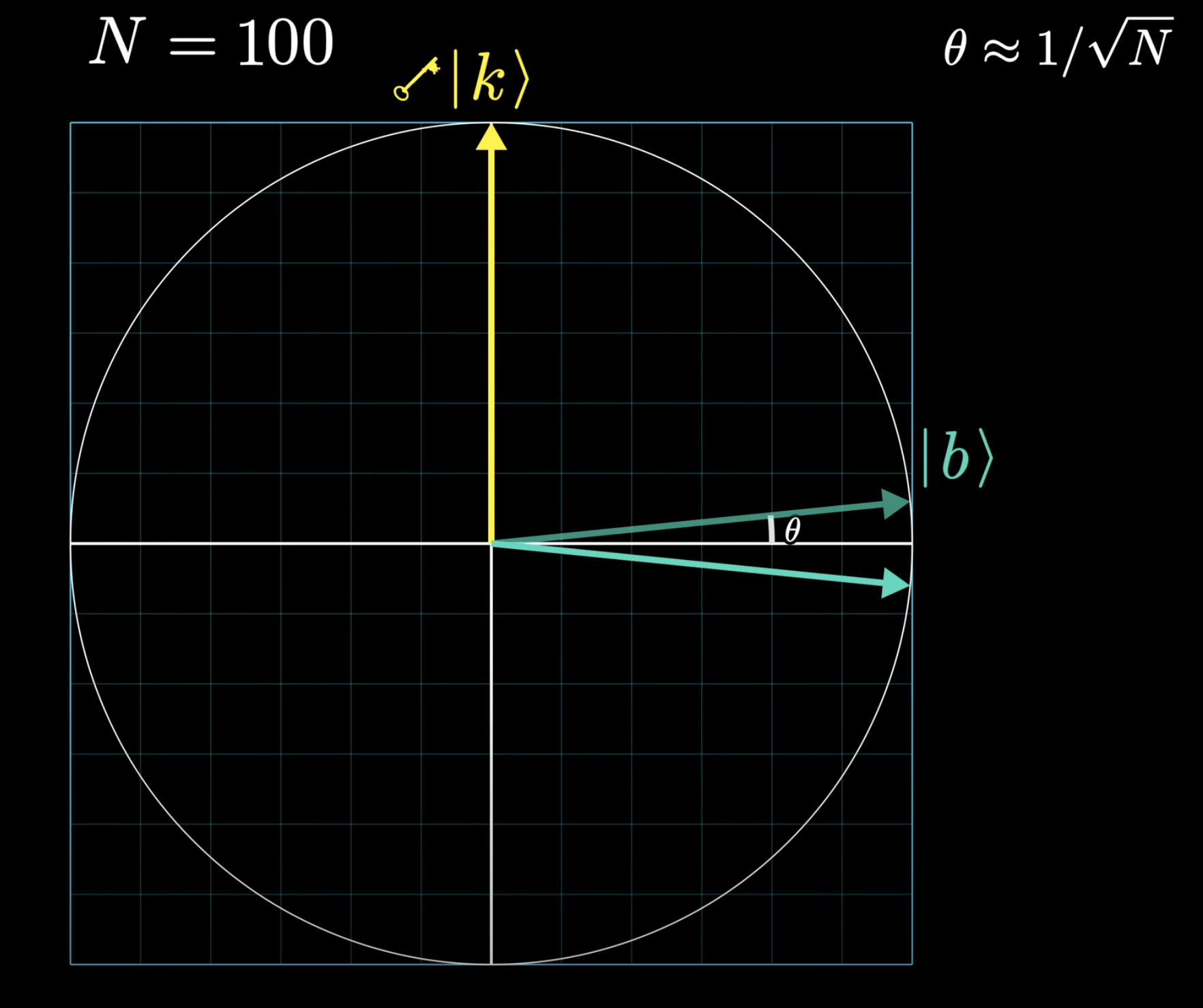
2. We can also have a quantum gate to have the vector flip around the balanced vector
3. Eventually the vector will get close to a the key vector after many steps

4 Something else

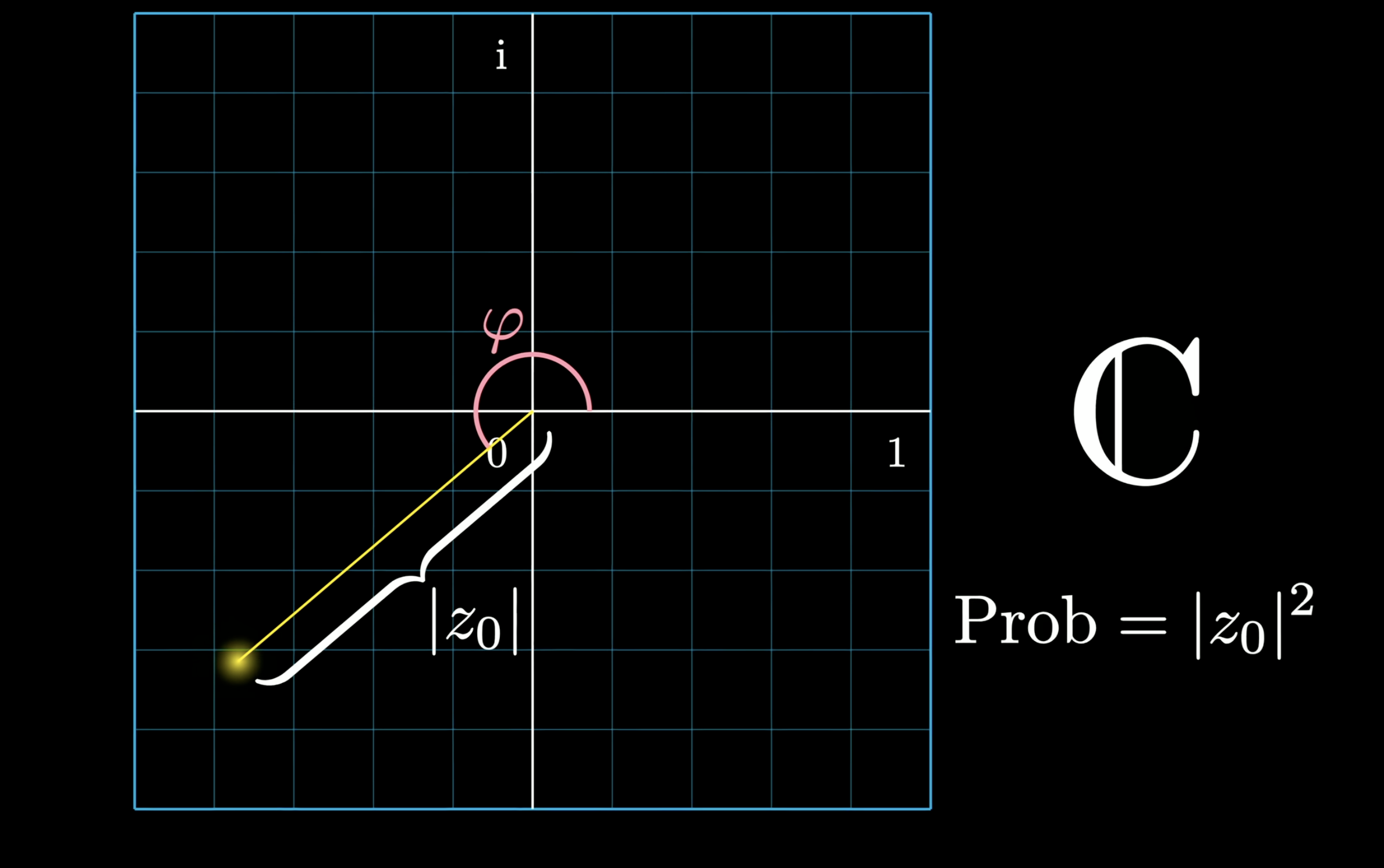
1. The state values are actually complex numbers instead of real. So we use the maglitude square to present prob. and the phase is more than just + and -
2. The Square is the speed up from quantum, sth like the diagonal distance is shorter… Taking it with a grain of salt
3. This is somewhat related to the block bouncing test to get Pi. will cover it later