Flow and Diffusion models Part 3 - Langevin and Matching

Lecture 3. Finished Lab 1, implemented flow and diffusion models and implemented Langevin Dynamics

0 Langevin Dynamics

Setting $p_t=p$ constant, and let $u^{target}=0$, we can a special case of Langevin Dynamics

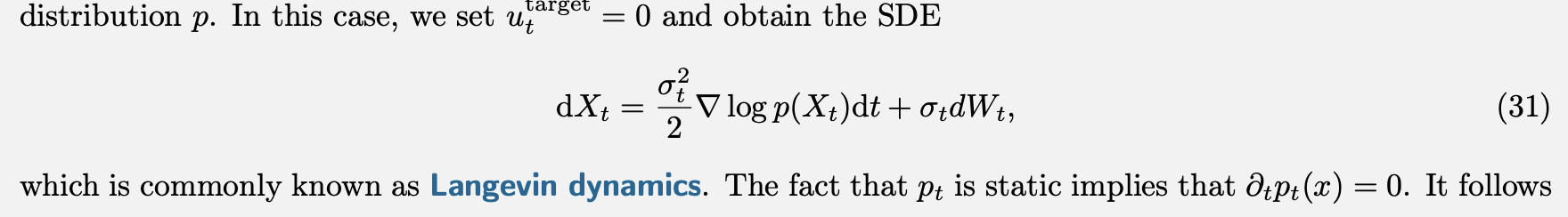
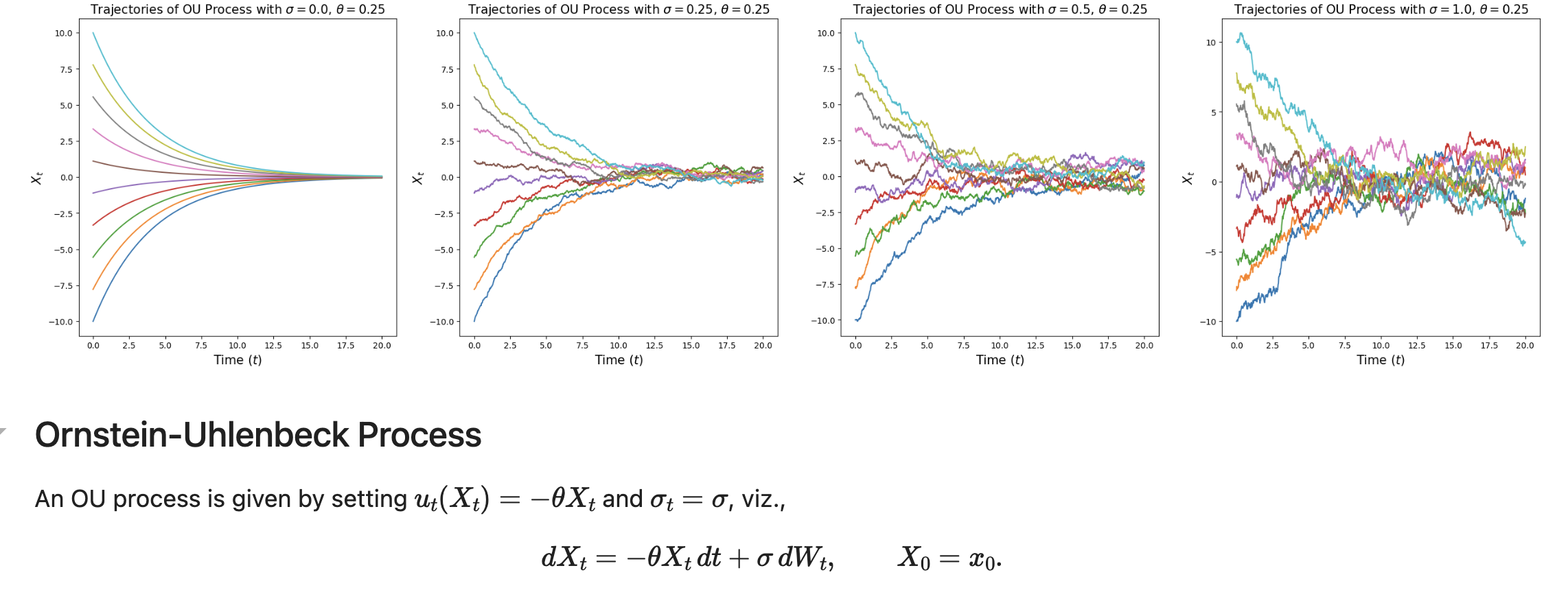
We can approve that it’s a special case of OU process when have zero mean and $\frac{\sigma^2}{2\theta}$ var

1 Flow Matching

Flow matching is actually vector field matching used for flow models Unfortunately, the marginal vector field is intractable, we have to turn to Conditional Flow Matching And we can approve these two loss are only differ by a constant,

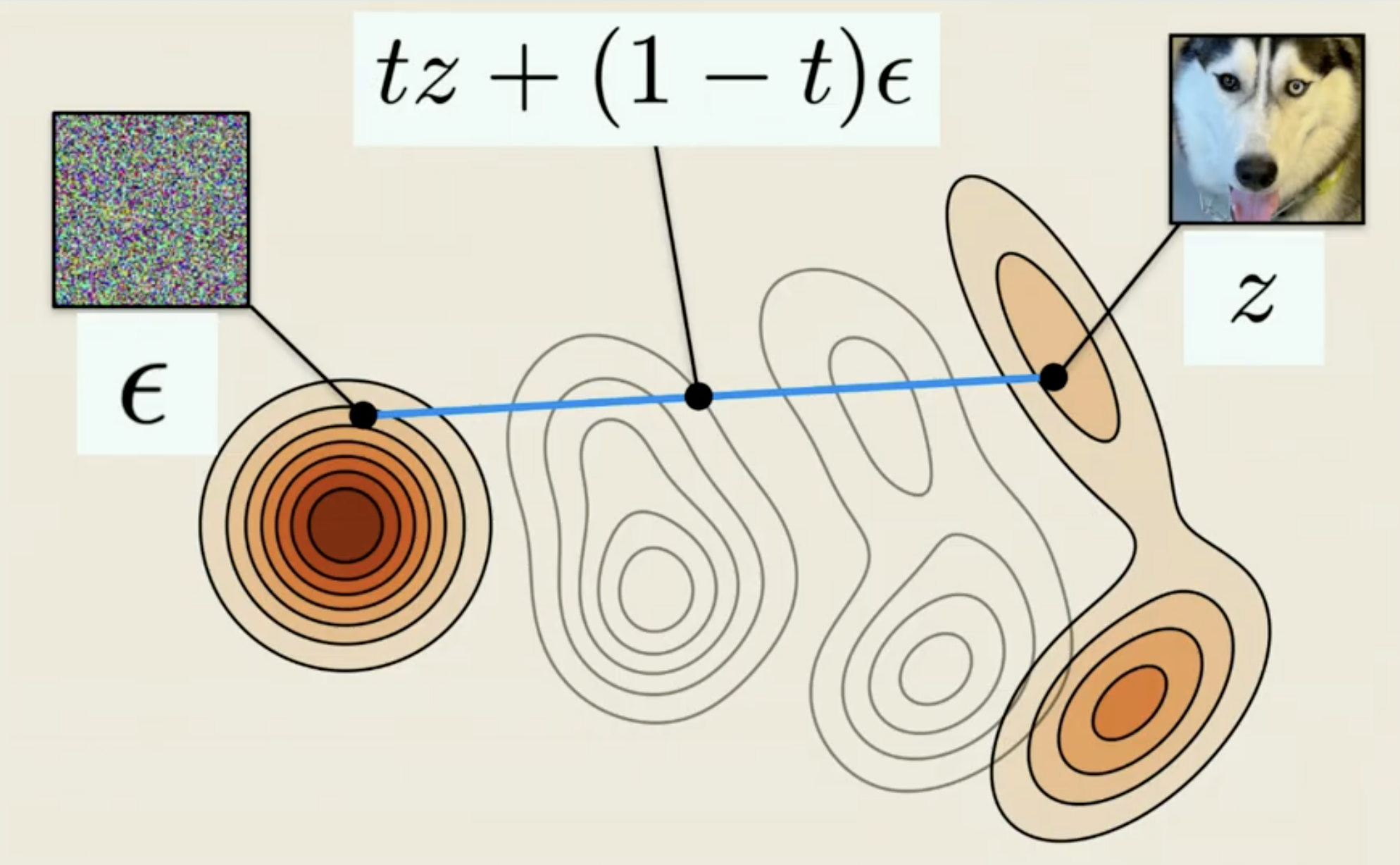
Here is an example of applying to Guassion case With chosen noise schedular, we can get the CondOT, Optimal Transport (OT) The final formula is actually so simple, using a network to matching a straightline

2 Score Matching

Very similiarly, we can use conditional score matching, which is called denoising score matching to replace intractable marginal score matching. and the loss functions are only diff by a constant

In the Gaussian example, you can also get a simply expression In the DDPM paper, it actually is the same with the formula above. This is more straighforward as prediction for the noise. Now we can get the algrithm for training. Still not sure how the plus sign in the loss function works for score matching. predicting the nagative noise?

After getting both vector field by flow matching, and score function by score matching, we can get the final formula for SDE. But in pratice, you only need to train one model, score function, instead of two 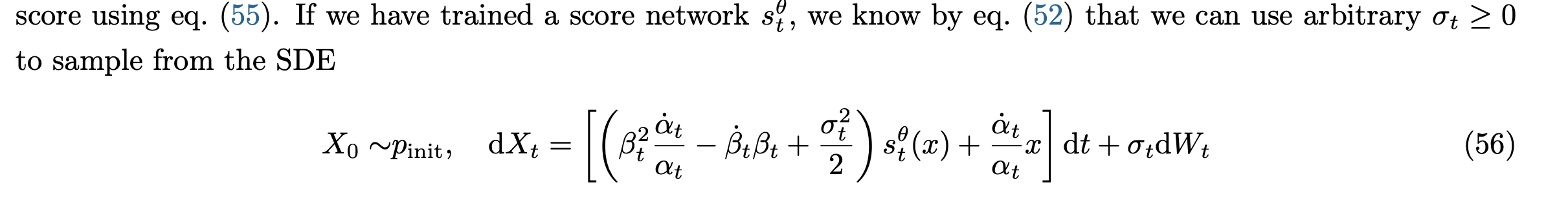Because simple algebra can get the conversion of these two