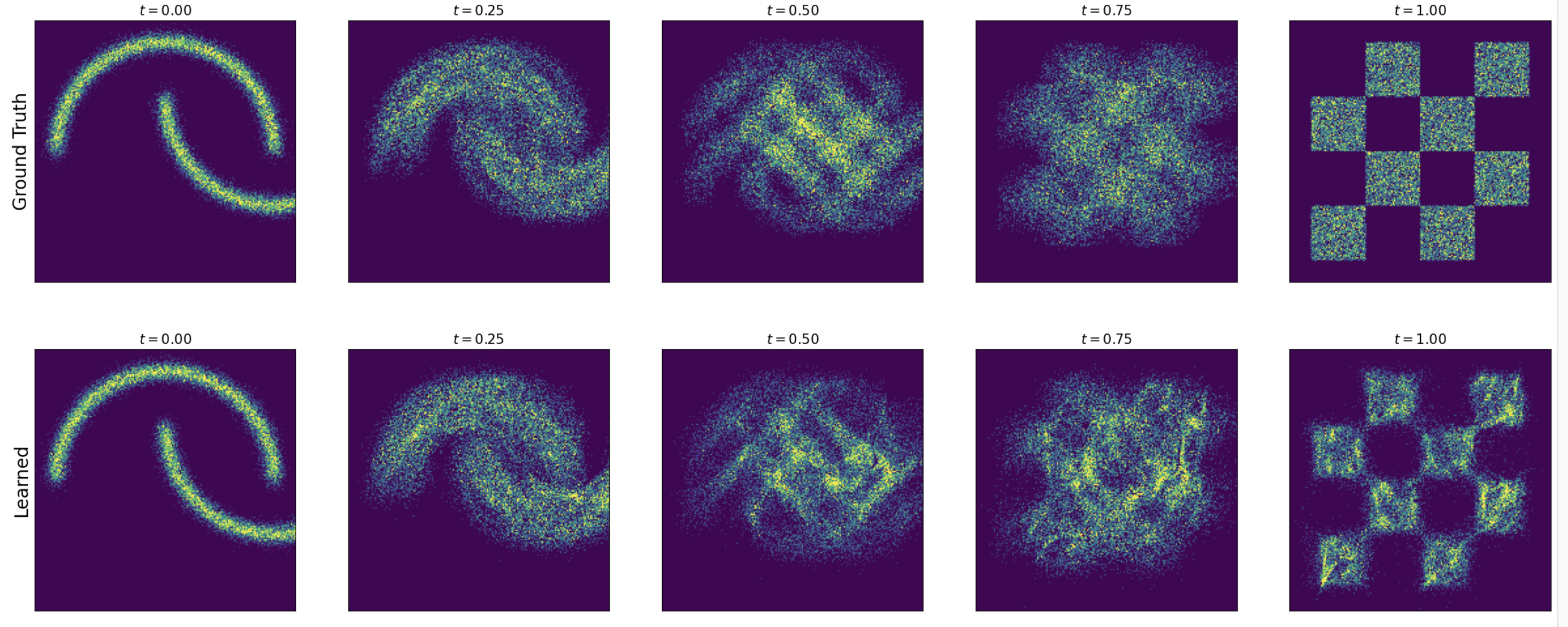
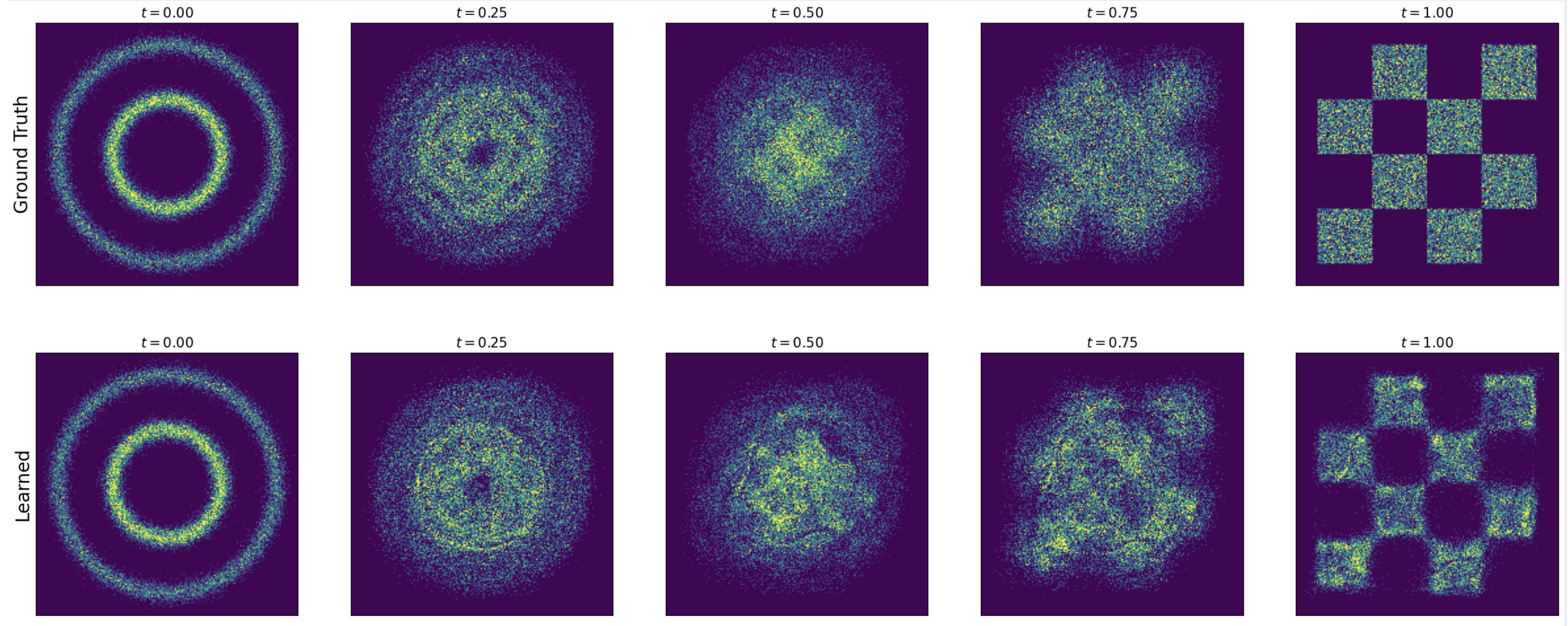
Flow and Diffusion models Lab 2-2 - Gaussian Probability Path w Score matching

I separat the score matching part from the Lab 2 and all put into this blog. So we can see more clearly how it works

1 Score Matching using Conditional Scores

Analytically, the score function is defined as $\nabla_x \log p_t(x|z) = \nabla_x N(x;\alpha_t z,\beta_t^2 I_d) = \frac{\alpha_t z - x}{\beta_t^2}.$

class GaussianConditionalProbabilityPath(ConditionalProbabilityPath):
  ...
  def conditional_score(self, x: torch.Tensor, z: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        """
        Evaluates the conditional score of p_t(x|z) = N(alpha_t * z, beta_t**2 * I_d)
        Note: Only defined on t in [0,1)
        Args:
            - x: position variable (num_samples, dim)
            - z: conditioning variable (num_samples, dim)
            - t: time (num_samples, 1)
        Returns:
            - conditional_score: conditional score (num_samples, dim)
        """ 
        alpha_t = self.alpha(t)
        beta_t = self.beta(t)
        return (z * alpha_t - x) / beta_t ** 2 

Define the SDE by adding Langevin Dynamics to the ODE function. \(d X_t = \left[u_t(X_t|z) + \frac{1}{2}\sigma^2 \nabla_x \log p_t(X_t|z) \right]dt + \sigma\, dW_t, \quad \quad X_0 = x_0 \sim p_{\text{simple}},\)

class ConditionalVectorFieldSDE(SDE):
    def __init__(self, path: ConditionalProbabilityPath, z: torch.Tensor, sigma: float):
        """
        Args:
        - path: the ConditionalProbabilityPath object to which this vector field corresponds
        - z: the conditioning variable, (1, ...)
        """
        super().__init__()
        self.path = path
        self.z = z
        self.sigma = sigma
    def drift_coefficient(self, x: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        bs = x.shape[0]
        z = self.z.expand(bs, *self.z.shape[1:])
        return self.path.conditional_vector_field(x,z,t) + 0.5 * self.sigma**2 * self.path.conditional_score(x,z,t)
    def diffusion_coefficient(self, x: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        return self.sigma * torch.randn_like(x)

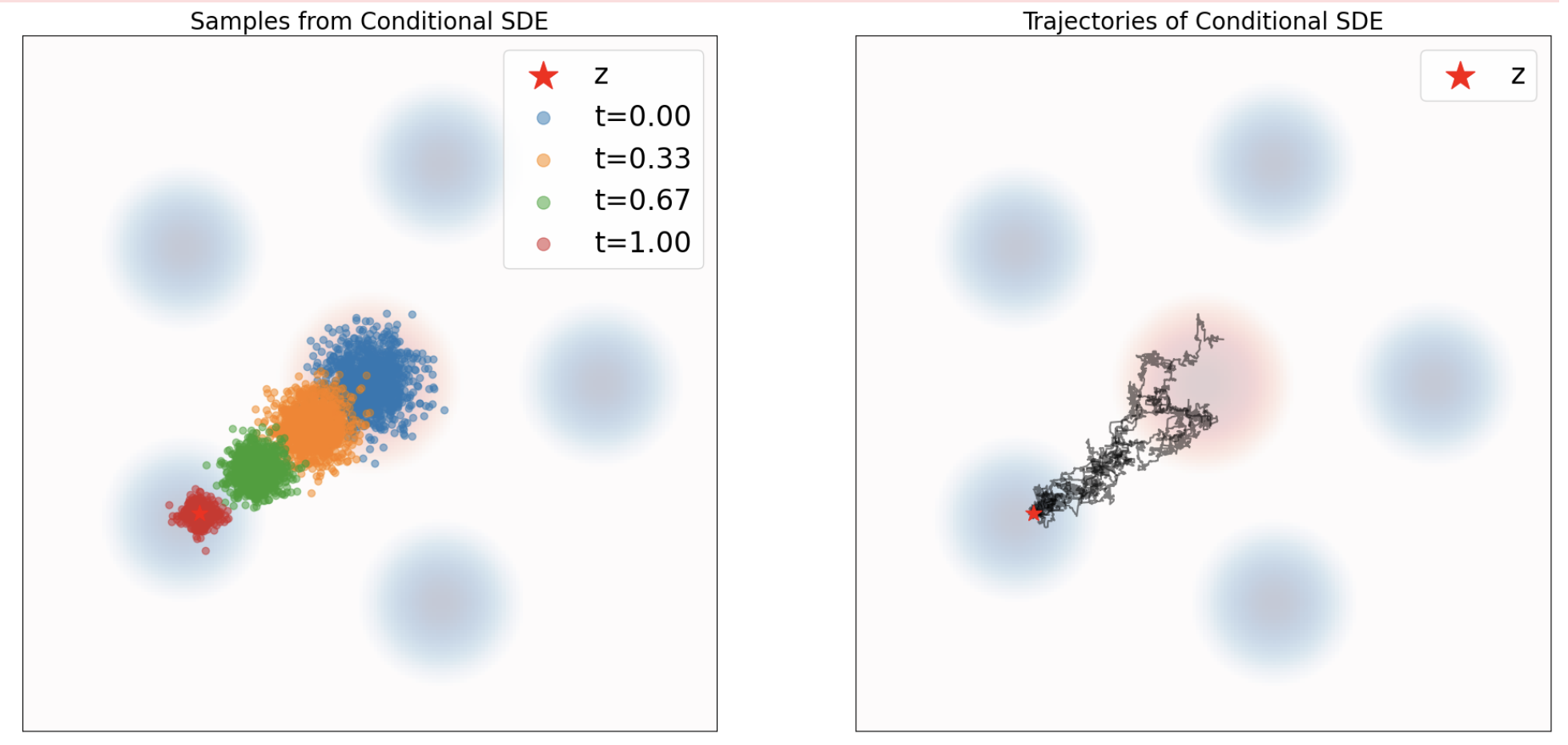
Now similar to ODE, you can plot every nth xts and all xts for trajectory

sde = ConditionalVectorFieldSDE(path, z, sigma)
simulator = EulerMaruyamaSimulator(sde)
x0 = path.p_simple.sample(num_samples) # (num_samples, 2)
ts = torch.linspace(0.0, 1.0, num_timesteps).view(1,-1,1).expand(num_samples,-1,1).to(device) # (num_samples, nts, 1)
xts = simulator.simulate_with_trajectory(x0, ts) # (bs, nts, dim)

2 Training score matching

Similarly to flow matching, the loss based on marginal score matching is a constant plus loss of conditional score matching, so we can traing the marginal score based on the loss of conditional score. \(\mathcal{L}_{\text{CSM}}(\theta) \triangleq \mathbb{E}_{t \sim \mathcal{U}[0,1), z \sim p(z), x \sim p_t(x|z)} \left[\lVert s_t^{\theta}(x) - \nabla \log p_t(x|z)\rVert^2\right]\)

• z is sampled from p_data
• t is sampled from torch.rand
• x is sampled from path.sample_conditional_path(z, t), same as groundtruth
• s_ref is get from self.path.conditional_score(x,z,t)

  class ConditionalScoreMatchingTrainer(Trainer):
    def __init__(self, path: ConditionalProbabilityPath, model: MLPScore, **kwargs):
        super().__init__(model, **kwargs)
        self.path = path
    def get_train_loss(self, batch_size: int) -> torch.Tensor:
        z = self.path.p_data.sample(batch_size) # (bs, dim)
        t = torch.rand(batch_size,1).to(z) # (bs, 1)
        x = self.path.sample_conditional_path(z,t) # (bs, dim)
        s_theta = self.model(x,t) # (bs, dim)
        s_ref = self.path.conditional_score(x,z,t) # (bs, dim)
        mse = torch.sum(torch.square(s_theta - s_ref), dim=-1) # (bs,)
        return torch.mean(mse)
  

  After the model is trained through MLP, generating a score_model, we can define the SDE together with flow_model from ODE training.

  class LangevinFlowSDE(SDE):
    def __init__(self, flow_model: MLPVectorField, score_model: MLPScore, sigma: float):
        super().__init__()
        self.flow_model = flow_model
        self.score_model = score_model
        self.sigma = sigma
    def drift_coefficient(self, x: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        return self.flow_model(x,t) + 0.5 * self.sigma ** 2 * self.score_model(x, t)
    def diffusion_coefficient(self, x: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        return self.sigma * torch.randn_like(x)
  

  Here is how we get the marginal probability path xts

  # Construct integrator and plot trajectories
  sde = LangevinFlowSDE(flow_model, score_model, sigma)
  simulator = EulerMaruyamaSimulator(sde)
  x0 = path.p_simple.sample(num_samples) # (num_samples, 2)
  ts = torch.linspace(0.0, 1.0, num_timesteps).view(1,-1,1).expand(num_samples,-1,1).to(device) # (num_samples, nts, 1)
  xts = simulator.simulate_with_trajectory(x0, ts) # (bs, nts, dim)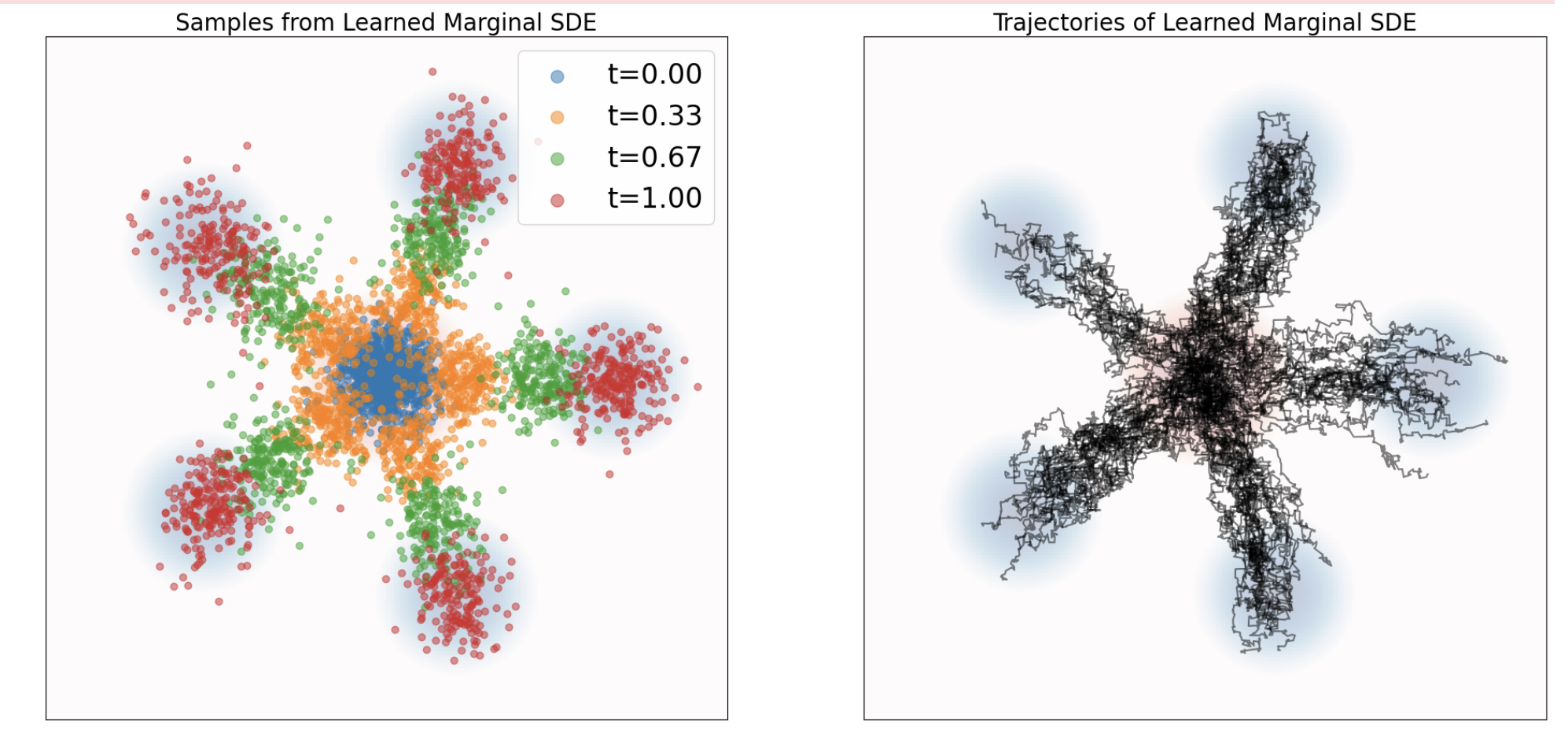
  

  

3 Get Score from Flow

Score can be calculated from Flow model, and implemented as below

class ScoreFromVectorField(torch.nn.Module):
    """
    Parameterization of score via learned vector field (for the special case of a Gaussian conditional probability path)
    """
    def __init__(self, vector_field: MLPVectorField, alpha: Alpha, beta: Beta):
        super().__init__()
        self.vector_field = vector_field
        self.alpha = alpha
        self.beta = beta
    def forward(self, x: torch.Tensor, t: torch.Tensor):
        """
        Args:
        - x: (bs, dim)
        Returns:
        - score: (bs, dim)
        """
        alpha_t = self.alpha(t)
        beta_t = self.beta(t)
        dt_alpha_t = self.alpha.dt(t)
        dt_beta_t = self.beta.dt(t)
        num = alpha_t * self.vector_field(x,t) - dt_alpha_t * x
        den = beta_t ** 2 * dt_alpha_t - alpha_t * dt_beta_t * beta_t
        return num / den   

4 Linear Probablity Path

At last, let’s try out a simple form of prabablity path, which does NOT require a guassian distribution for the $p_{init}$. But it does NOT have a closed form for the conditional score neither.
The linear path is given by a linear interpolation between $X_0$ and $z$. \(X_t = (1-t) X_0 + tz\)

class LinearConditionalProbabilityPath(ConditionalProbabilityPath):
    def __init__(self, p_simple: Sampleable, p_data: Sampleable):
        super().__init__(p_simple, p_data)
    def sample_conditioning_variable(self, num_samples: int) -> torch.Tensor:
        return self.p_data.sample(num_samples)
    def sample_conditional_path(self, z: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        x0 = self.p_simple.sample(z.shape[0])
        return (1 - t) * x0 + t * z
    def conditional_vector_field(self, x: torch.Tensor, z: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        return (z - x) / (1 - t)
    def conditional_score(self, x: torch.Tensor, z: torch.Tensor, t: torch.Tensor) -> torch.Tensor:
        raise Exception("You should not be calling this function!")

Here is the derivation of vector field Here you can

• Graph conditional probability paths using sample_conditional_path as groundtruth xts = path.sample_conditional_path(zz, tt)
• Graph conditional probability paths using `conditional_vector_field from ODE

  ode = ConditionalVectorFieldODE(path, z)
  simulator = EulerSimulator(ode)
  ...
  x0 = path.p_simple.sample(num_samples)
  xts = simulator.simulate_with_trajectory(...)
  

• Graph conditional probability paths using sample_marginal_path :ts = path.sample_marginal_path(tt), which is actually sample_conditional_path with num_sample of points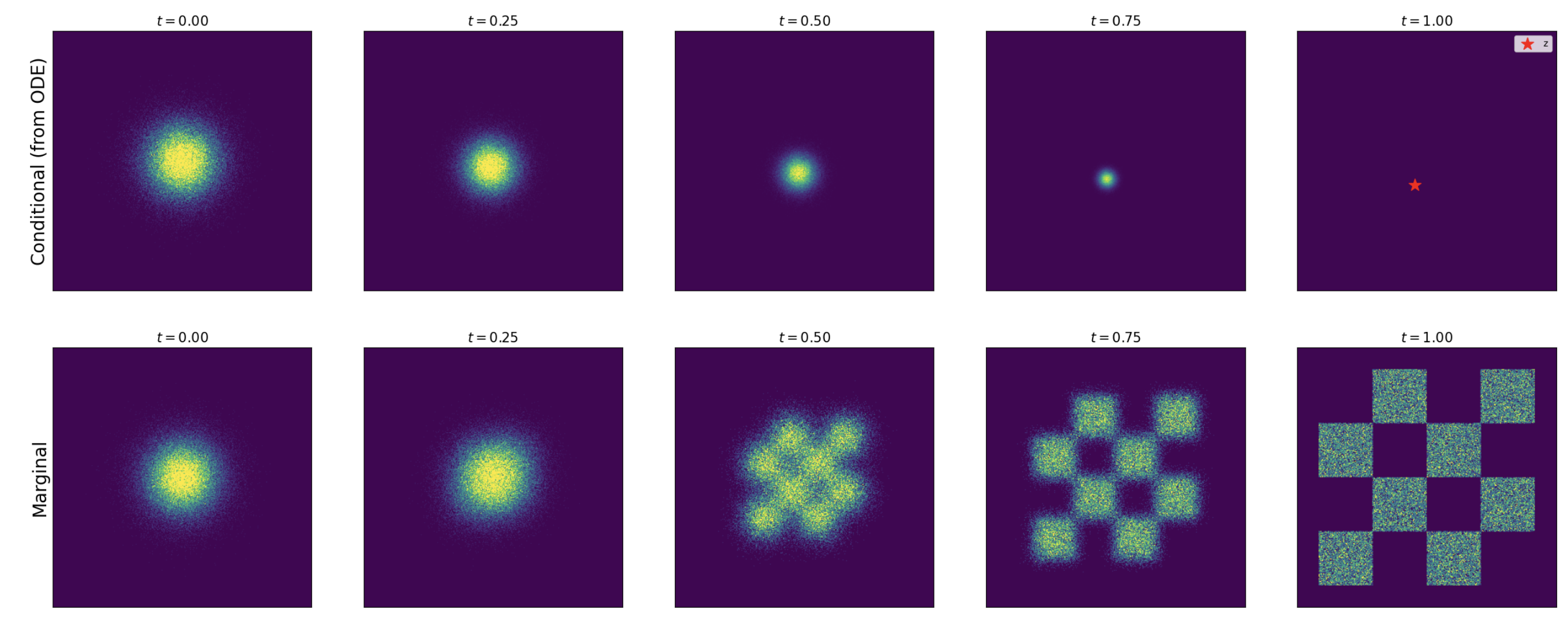

Arbitray $p_{init}$ can be used to get to $p_{data}$