Flow and Diffusion models Lab 3 (Mac GPU and backup w pickle)

Diffusion Lab3, conditional generation

0 Python object backup with Pickle

To use GPU on Mac, use mps as the device value.

device = 'mps' if torch.backends.mps.is_available() else 'cpu'

The training of Unet took a while so I saved the trained weights with pickle

import pickle
with open("unet.pkl", "wb") as file:
    # Use pickle.dump() to serialize the object and write it to the file
    pickle.dump(unet, file)

and the saved unet.pkl file can be loaded by

with open('unet.pkl', 'rb') as file:
    unet_reloaded = pickle.load(file)

1 MNIST

MNIST can be download online but torchvision.datasets download does NOT work no more. So we can google and download, put under root folder data

# data is put ./data/MNIST/raw/t10k-images-idx3-ubyte etc 
self.dataset = datasets.MNIST(
    root='./data',
    train=True,
    download=False,
    transform=transforms.Compose([
        transforms.Resize((32, 32)),
        transforms.ToTensor(),
        transforms.Normalize((0.5,), (0.5,)),
    ])
)

And use Gaussian conditional probabily path, we can construct the MNIST from random noise

num_samples = num_rows * num_cols
z, _ = path.p_data.sample(num_samples)
z = z.view(-1, 1, 32, 32)
# Sample from conditional probability paths and graph
ts = torch.linspace(0, 1, num_timesteps).to(device)
for tidx, t in enumerate(ts):
    tt = t.view(1,1,1,1).expand(num_samples, 1, 1, 1) # (num_samples, 1, 1, 1)
    xt = path.sample_conditional_path(z, tt) # (num_samples, 1, 32, 32)
    ...

2 Classifier Free Guidance

• Guidance Based on conditional on lable y, we can get the loss function for CFM \(\begin{align*}\mathcal{L}_{\text{CFM}}(\theta) &= \,\,\mathbb{E}_{\square} \lVert u_t^{\theta}(x|y) - u_t^{\text{ref}}(x|z)\rVert^2\\ \square &= z,y \sim p_{\text{data}}(z,y), x \sim p_t(x|z)\end{align*}\)
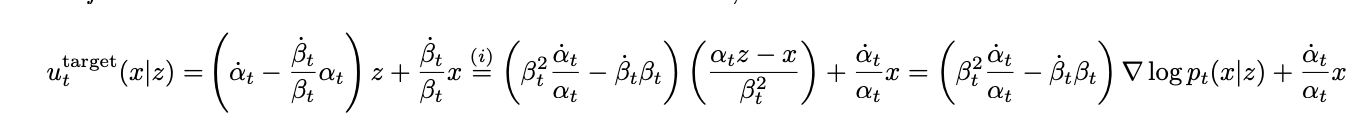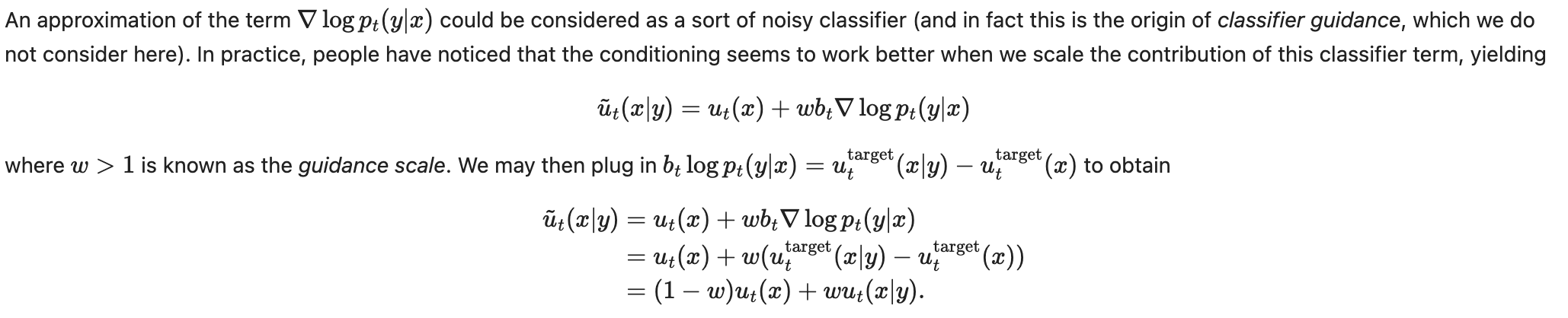• Classifier Free By algebra arrangement, we can get the relationship between vector field and score function With this relationship, we can get following results with a Bayesian formula applied and knowing $\nabla \log p_t(y)=0$ We some rearrangement, we can get from classifer guidence and a weight to following conclusion But we need to train 2 models, $u_t(x)$ and $u_t(x|y)$ Following trick can get only 1 model trained, which is classifer-free

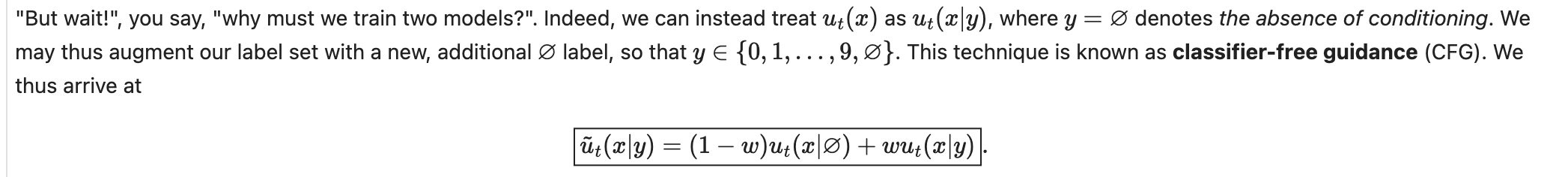
3 Implementation

First we define the drift parameter according the CFG formula. Notice that we use 10 as the void class (valid class is 0-9)

class CFGVectorFieldODE(ODE):
    def __init__(self, net: ConditionalVectorField, guidance_scale: float = 1.0):
        self.net = net
        self.guidance_scale = guidance_scale
    def drift_coefficient(self, x: torch.Tensor, t: torch.Tensor, y: torch.Tensor) -> torch.Tensor:
        """
        Args:
        - x: (bs, c, h, w)
        - t: (bs, 1, 1, 1)
        - y: (bs,)
        """
        guided_vector_field = self.net(x, t, y)
        unguided_y = torch.ones_like(y) * 10
        unguided_vector_field = self.net(x, t, unguided_y)
        return (1 - self.guidance_scale) * unguided_vector_field + self.guidance_scale * guided_vector_field

The training part define loss based on \(\begin{align*}\mathcal{L}_{\text{CFM}}(\theta) &= \,\,\mathbb{E}_{\square} \lVert u_t^{\theta}(x|y) - u_t^{\text{ref}}(x|z)\rVert^2\\ \square &= z,y \sim p_{\text{data}}(z,y), x \sim p_t(x|z),\,\text{replace $y$ with $\varnothing$ with probability $\eta$}\end{align*}\)

1. To sample an image $(z,y) \sim p_{\text{data}}$, use self.path.p_data.sample
2. You can generate a mask corresponding to “probability $\eta$” via mask = torch.rand(batch_size) < self.eta.
3. You can sample $t \sim \mathcal{U}[0,1]$ using torch.rand(batch_size, 1, 1, 1). Don’t mix up torch.rand with torch.randn!
4. You can sample $x \sim p_t(x|z)$ using self.path.sample_conditional_path.

   class CFGTrainer(Trainer):
    def __init__(self, path: GaussianConditionalProbabilityPath, model: ConditionalVectorField, eta: float, **kwargs):
        assert eta > 0 and eta < 1
        super().__init__(model, **kwargs)
        self.eta = eta
        self.path = path
   
    def get_train_loss(self, batch_size: int) -> torch.Tensor:
        # Step 1: Sample z,y from p_data
        z, y = self.path.p_data.sample(batch_size) # (bs, c, h, w), (bs,1)
        # Step 2: Set each label to 10 (i.e., null) with probability eta
        xi = torch.rand(y.shape[0]).to(y.device)
        y[xi < self.eta] = 10.0
        # Step 3: Sample t and x
        t = torch.rand(batch_size,1,1,1).to(z) # (bs, 1, 1, 1)
        x = self.path.sample_conditional_path(z,t) # (bs, 1, 32, 32)
        # Step 4: Regress and output loss
        ut_theta = self.model(x,t,y) # (bs, 1, 32, 32)
        ut_ref = self.path.conditional_vector_field(x,z,t) # (bs, 1, 32, 32)
        error = torch.einsum('bchw -> b', torch.square(ut_theta - ut_ref)) # (bs,)
        return torch.mean(error)
   

And here is the results after training. You can see that class 10 is getting random values

4 Unet structure

Skip this part