Langevin Sampling in Diffuion models

This youtuber only uploaded 3 videos and one of them explained score matching better than any others and finally I am ready to read Dr Yang Song’s paper and blog

0 Model Classifications

• Likelihood-based models, which directly learn the distribution’s PDF via (approximate) maximum likelihood., like AR, VAEs, EBMs and normalizing flow models
• Implicit generative models, where the probability distribution is implicitly represented by a model of its sampling process, like GAN

1 Langevin Sampling

To sample from a distribution w known pdf, we can use following algorithm: 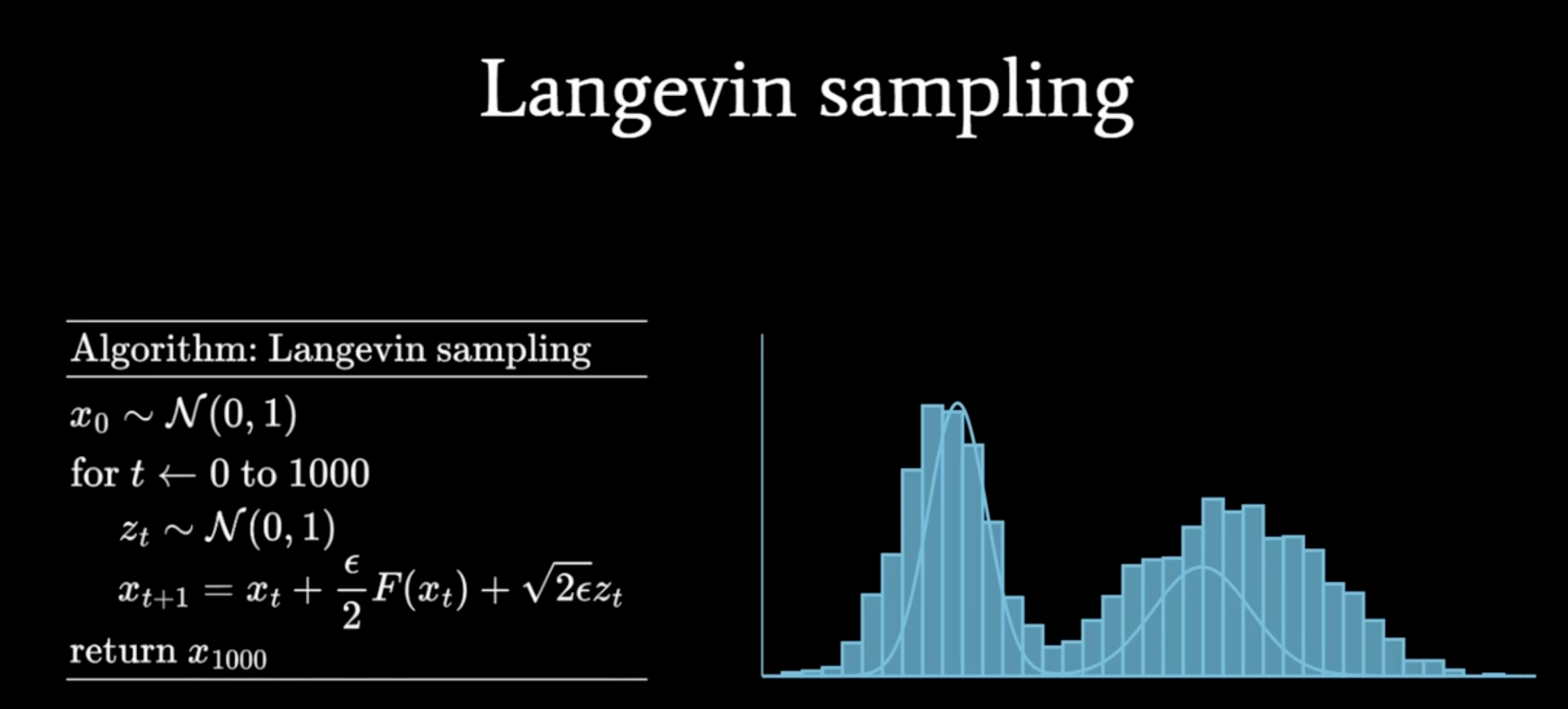where $F(x)=\nabla_x\log(p(x))$, is just the score function Here is the sample code of running Langevin Sampling on a uniform distribution over dice rolling Here are 2 things to notice

1. Why we need the log? It can make sure converge fast, especially when p(x) is small 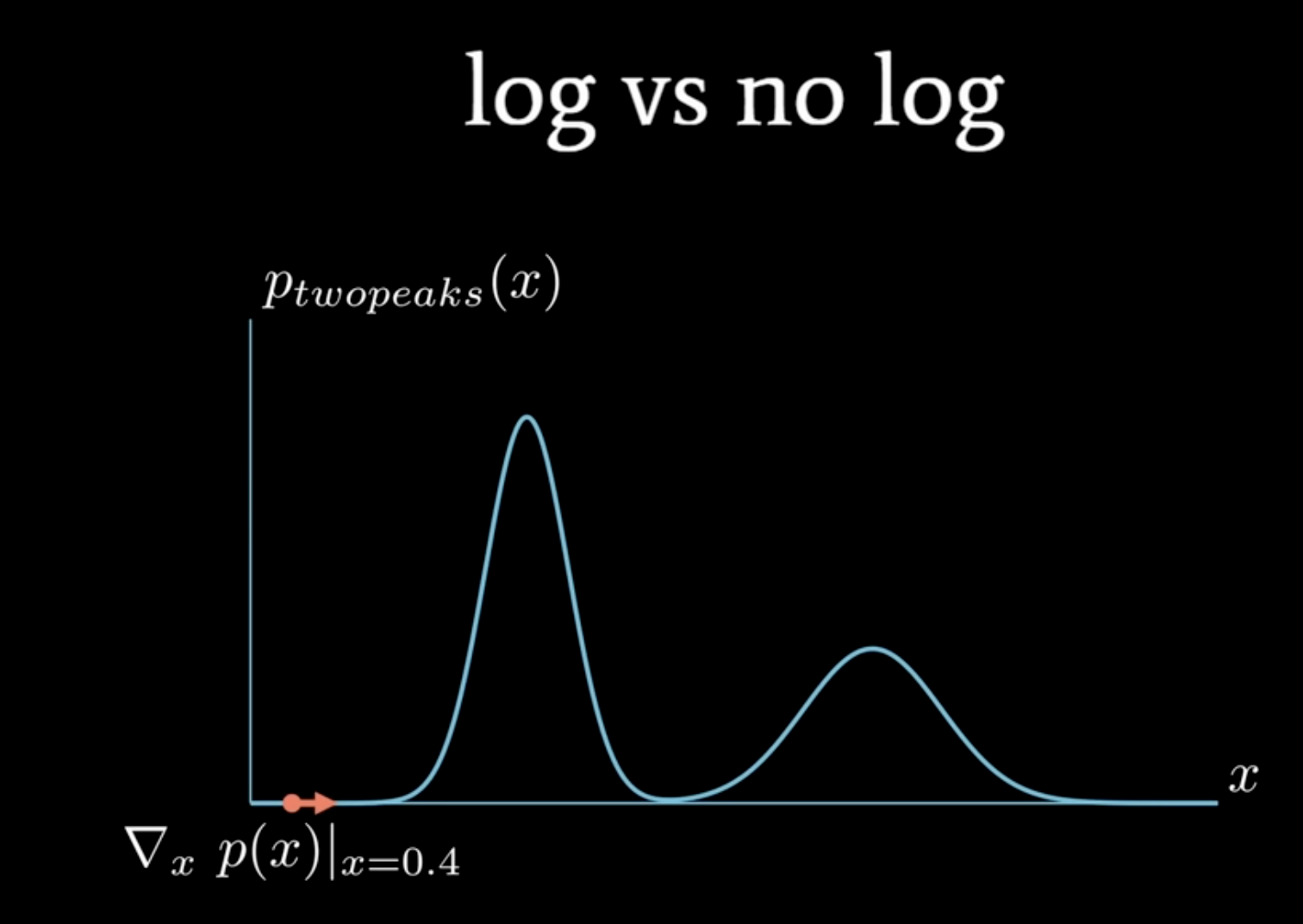\(F(x)= \frac{d}{dx}\log(p(x)) \\ =\frac{p(x)}{p(x)} \\ =\frac{\nabla_xp(x)}{p(x)}\)
2. The noise term is to make sure we are getting a distribution, rather than focused on highest percentage points. 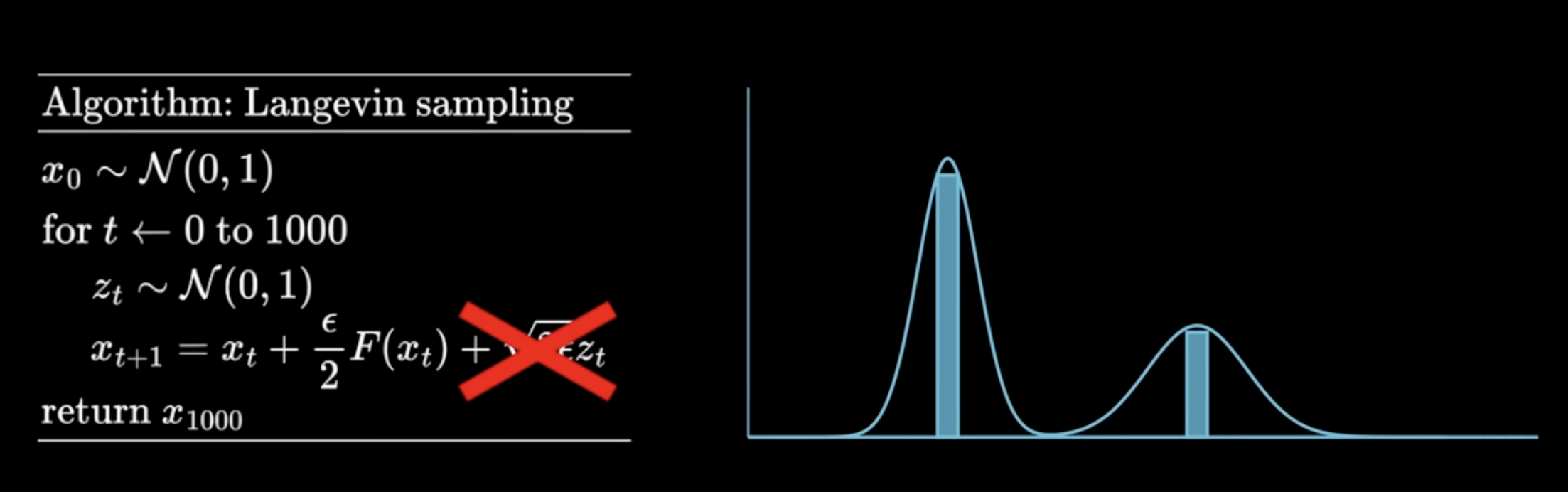What if the PDF is unknown? That’s where DL comes to the rescue

   2 Image Generation

   Recap this youtubers’ first video on diffusion, the idea is very straightforward.

   • Diffusion process is highly similar to ML training process
   • Predicting noise, is actually finding the direction to the valid image cluster in the image space The noise is playing a critical role in the diffusion models in following ways
3. As we shown above, ensure diversity. and also avoid local optima, anohter ML similarity
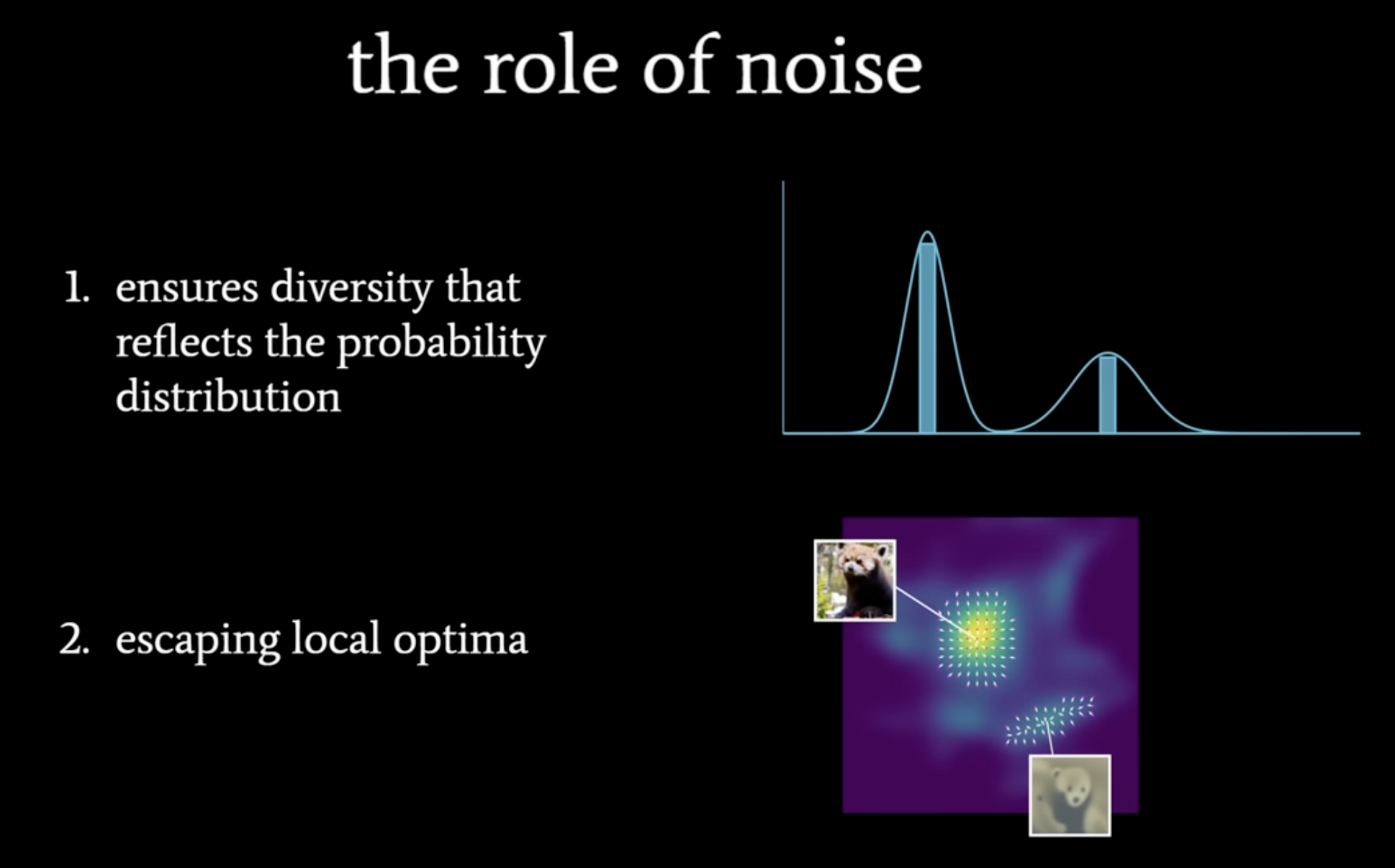
4. If we remove the noise, you will see the blurr image. which is explained in previous blog
5. The diffusion is for “logical” part, and noise is for creativity So now you will see diffusion is essencially same as finding the weight in DL training