Bezier Curves
This is one of most amazing videos for math concept introduction，together with a great primer
0 Defination
Lerp means Linear interpolation.
\(P(t) = (1-t)P_0 + tP_1\)
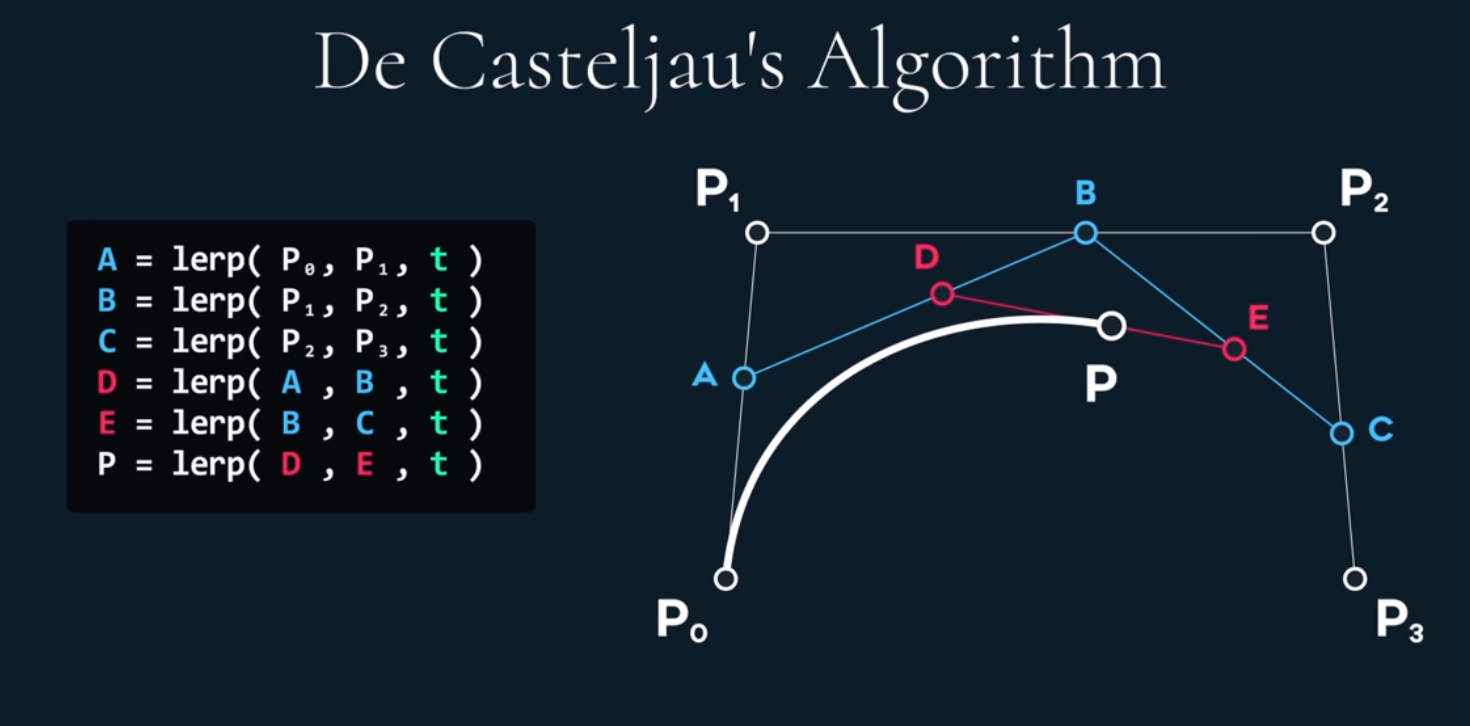
De Casteljau defination of Bezier curves is illustrated below with recursive lerps.
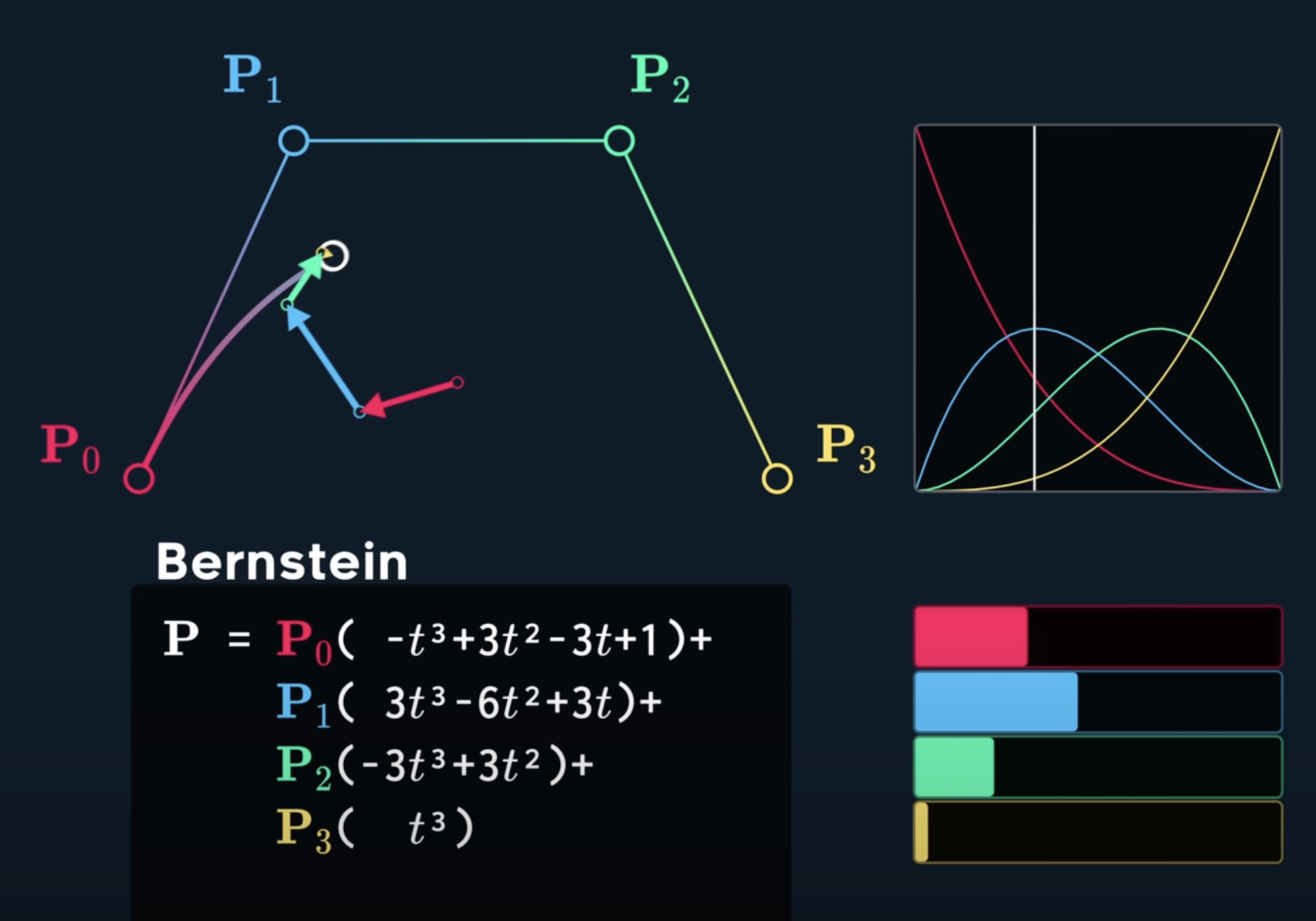
Separeting the $P$ values, gives you basis of Bezier functions
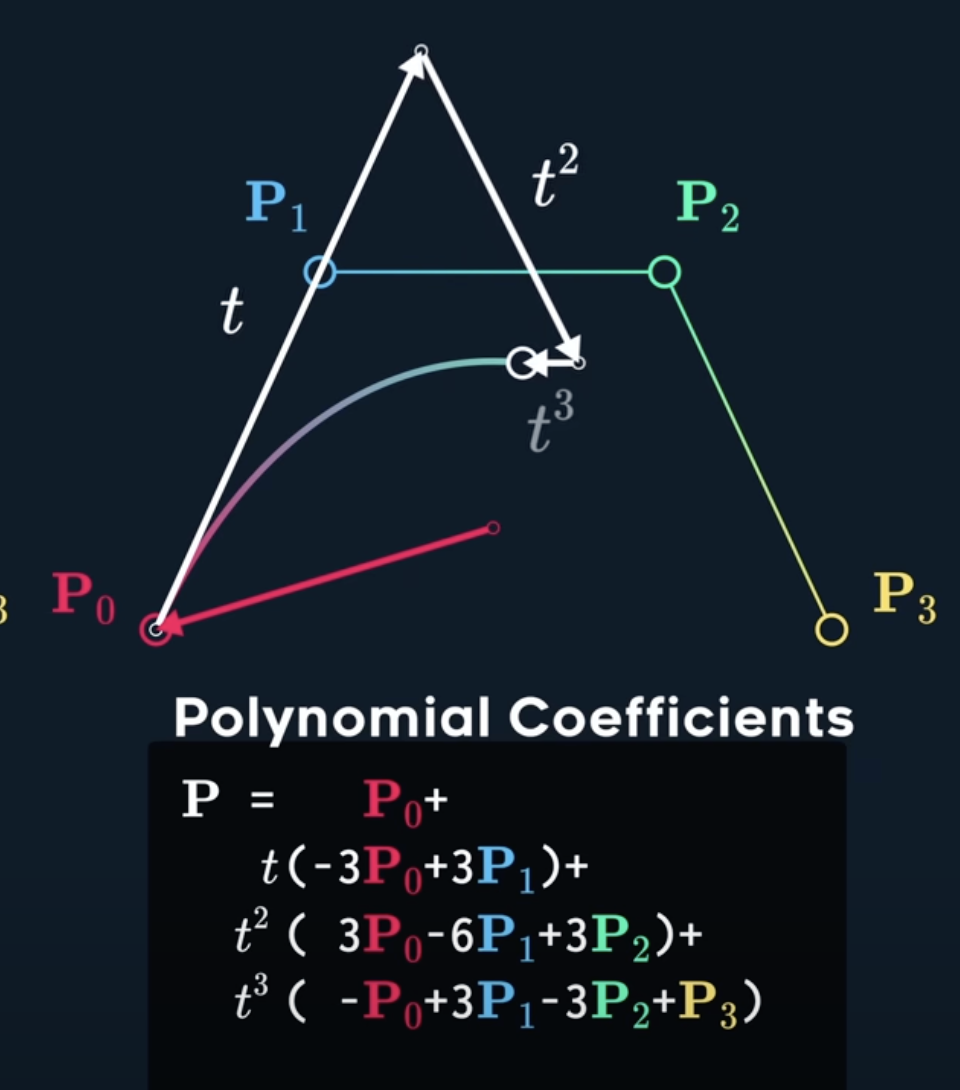
Two other definatinos are listed as polynomial coefficient and Matrix form
1. B-Spline
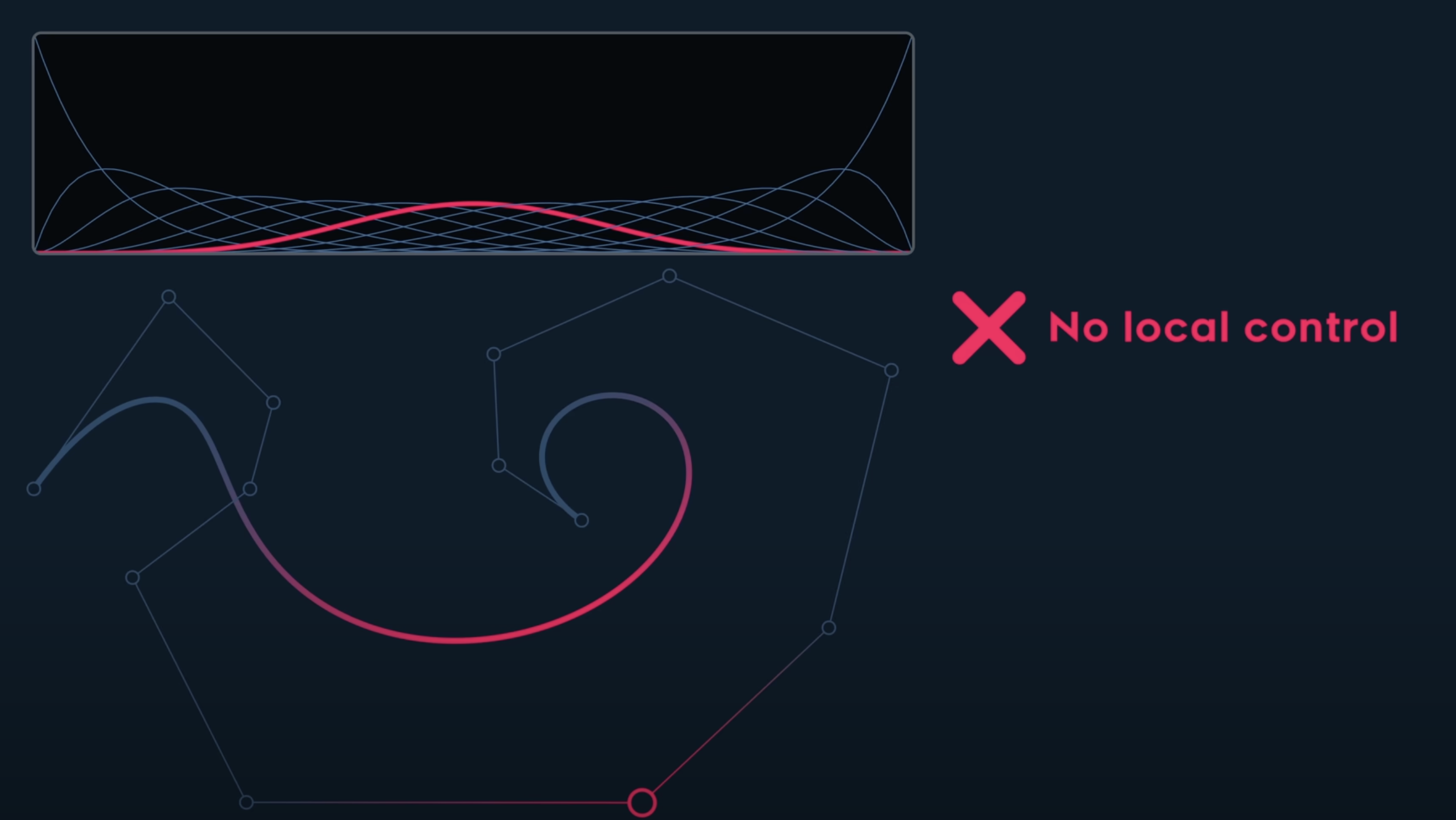
The shortage of Bezier curves are
- No local control (The basis covers the whole range)
- Does NOT interpolate (except for start/end points)
- Unstable and expensive to calculate
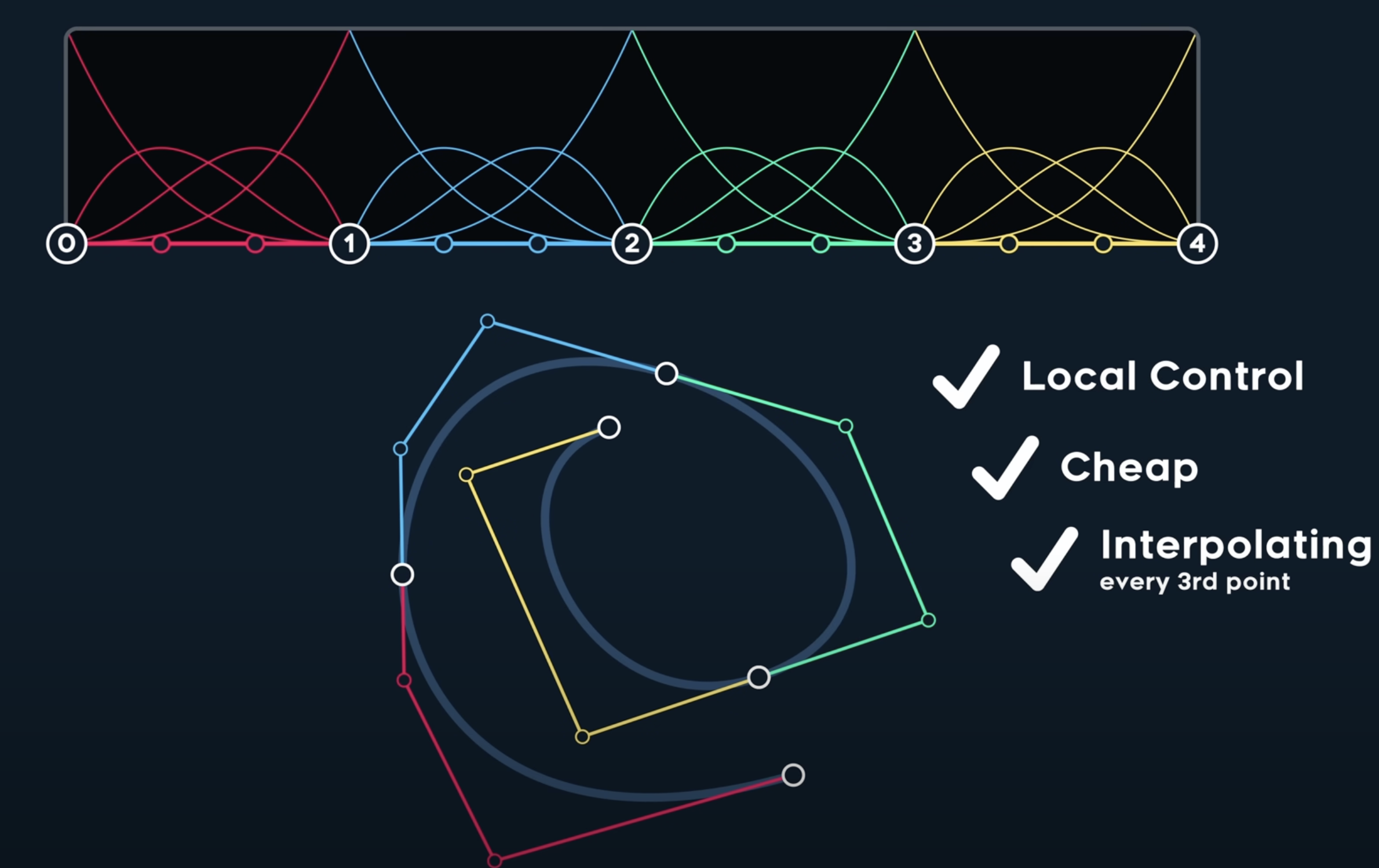
and the B-Spline solves all these issues
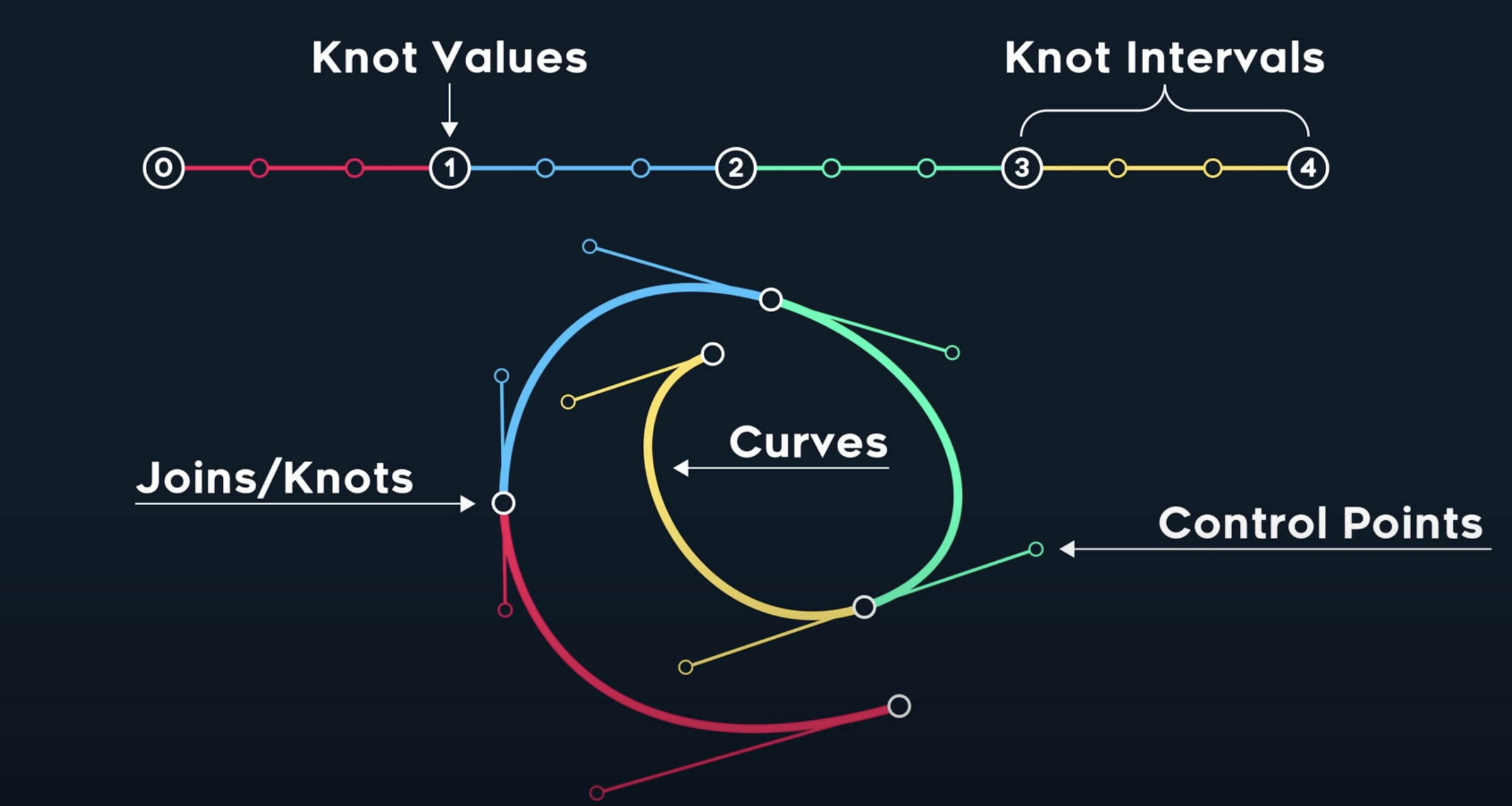
We only consider equal knot interval B-splines
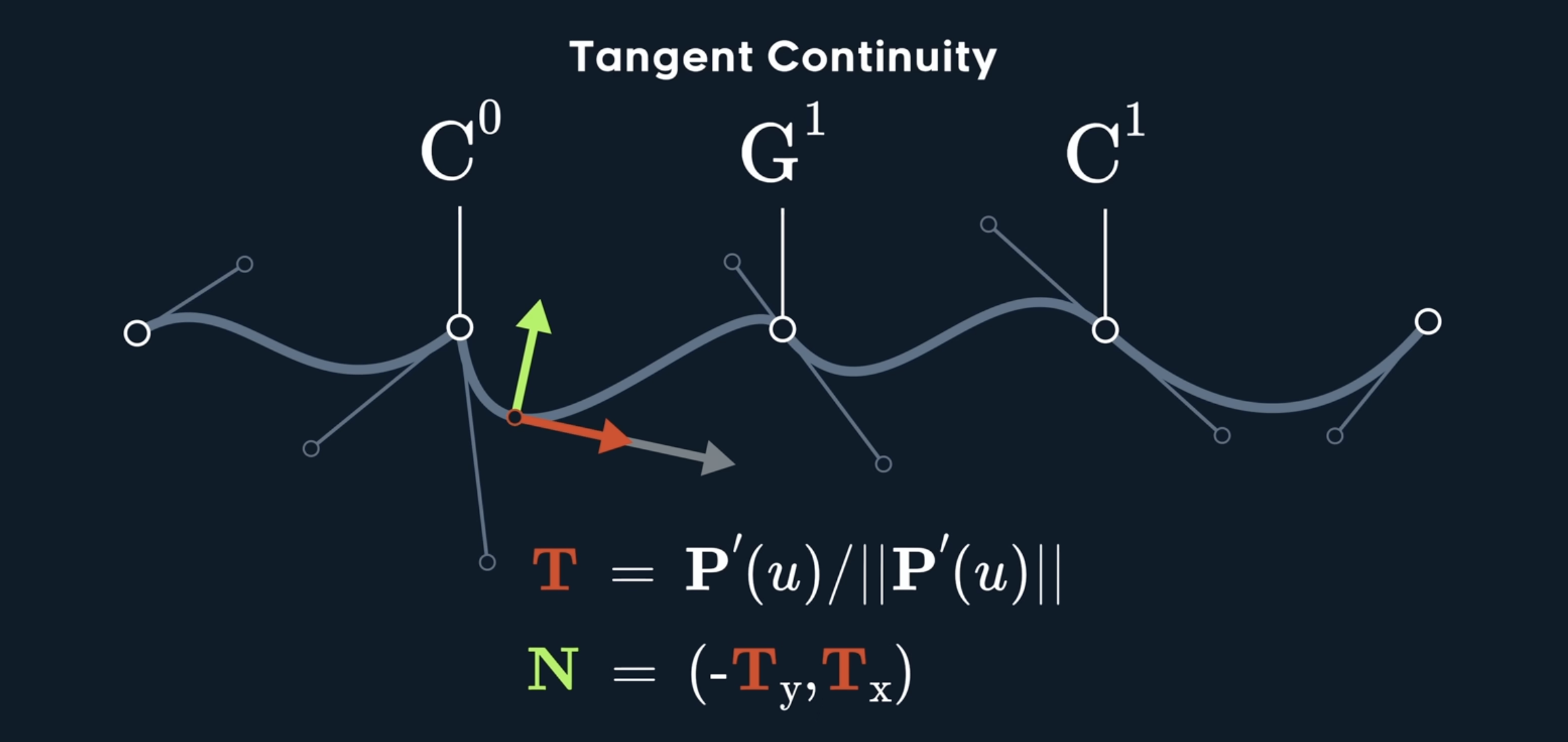
2. Parametric Continuity
$C^i$ continuous if \(A^{(i)}(t_{end})=B^{(i)}(t_{start}) \\ i={0,1,..n}\)
The continuity of B-spline is decided by the control points next to the knots.
Broken and Aligned knots give $C^0$
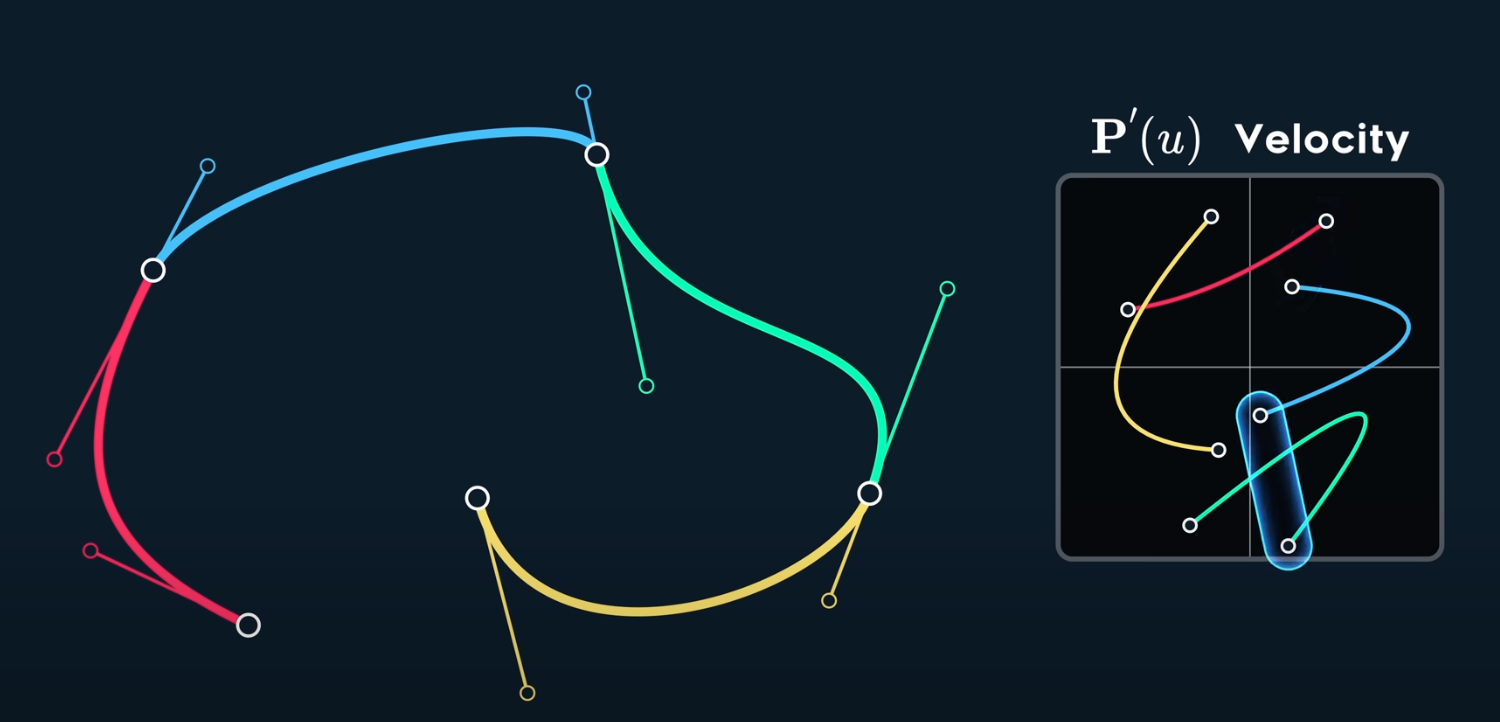To get continuous velcocity, $P_4$ can NOT be random.
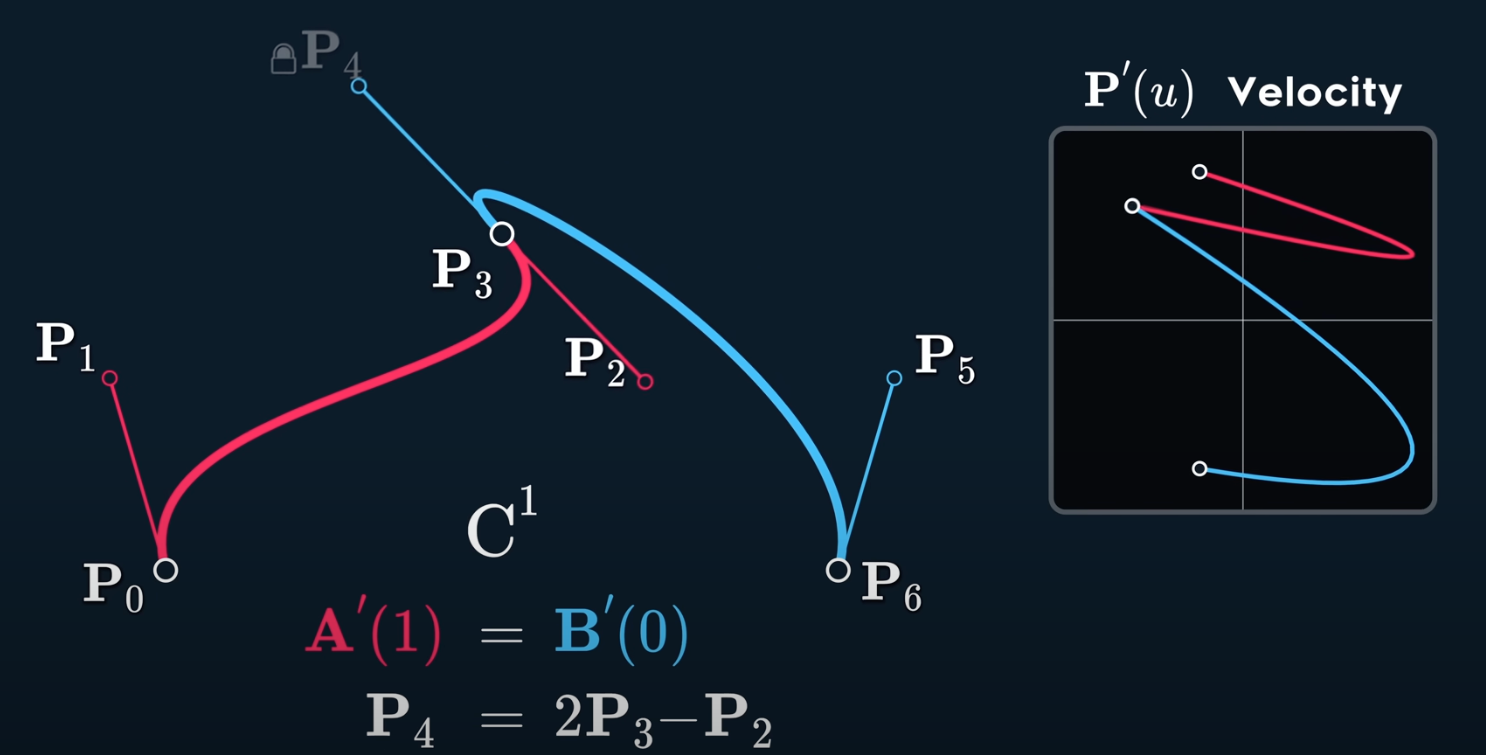So, mirrored knots gives $C^1$ but NOT $C^2$
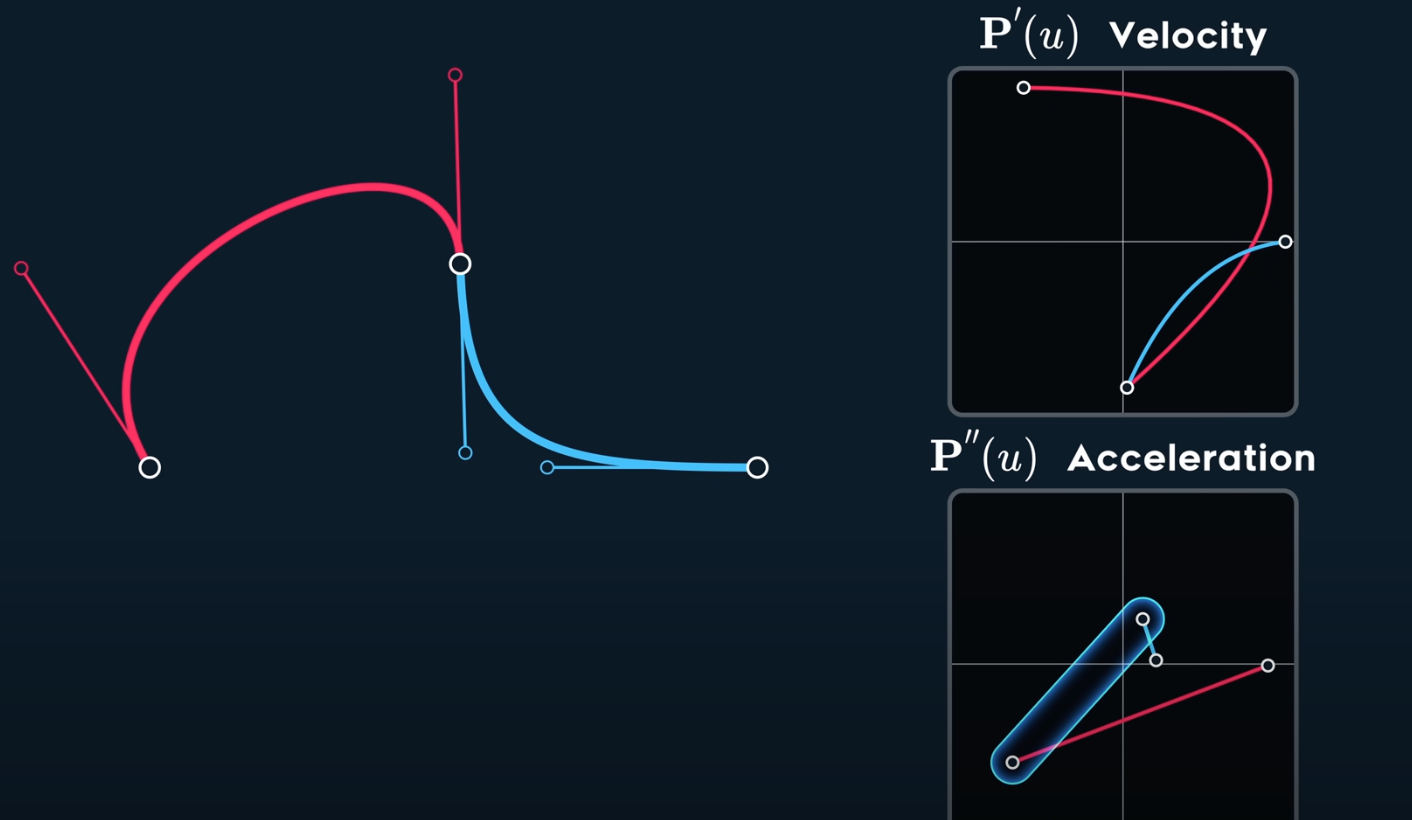To get $C^2$, $P_5$ is locked
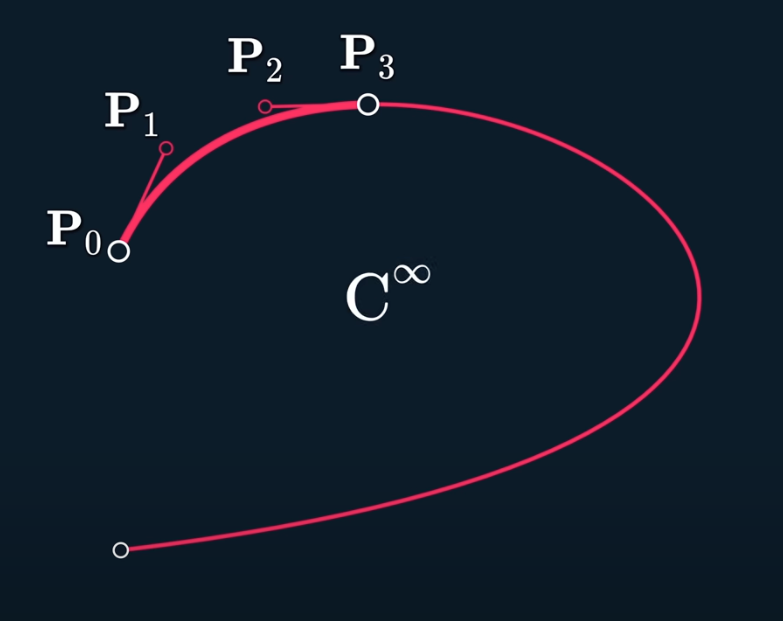
$C^3$ gives you totally no control of the curve, and super sensative to the initial conditions.
And it’s same as extrapolating t to larger than 1 values.
So it’s not just $C^3$ but $C^\infin$
3 Geometry Continuity
For Aligned knots, if we ignore the magnitude of the velocity, and only looks at unit vector and it’s norm, it’s still continuous and called $G^1$.
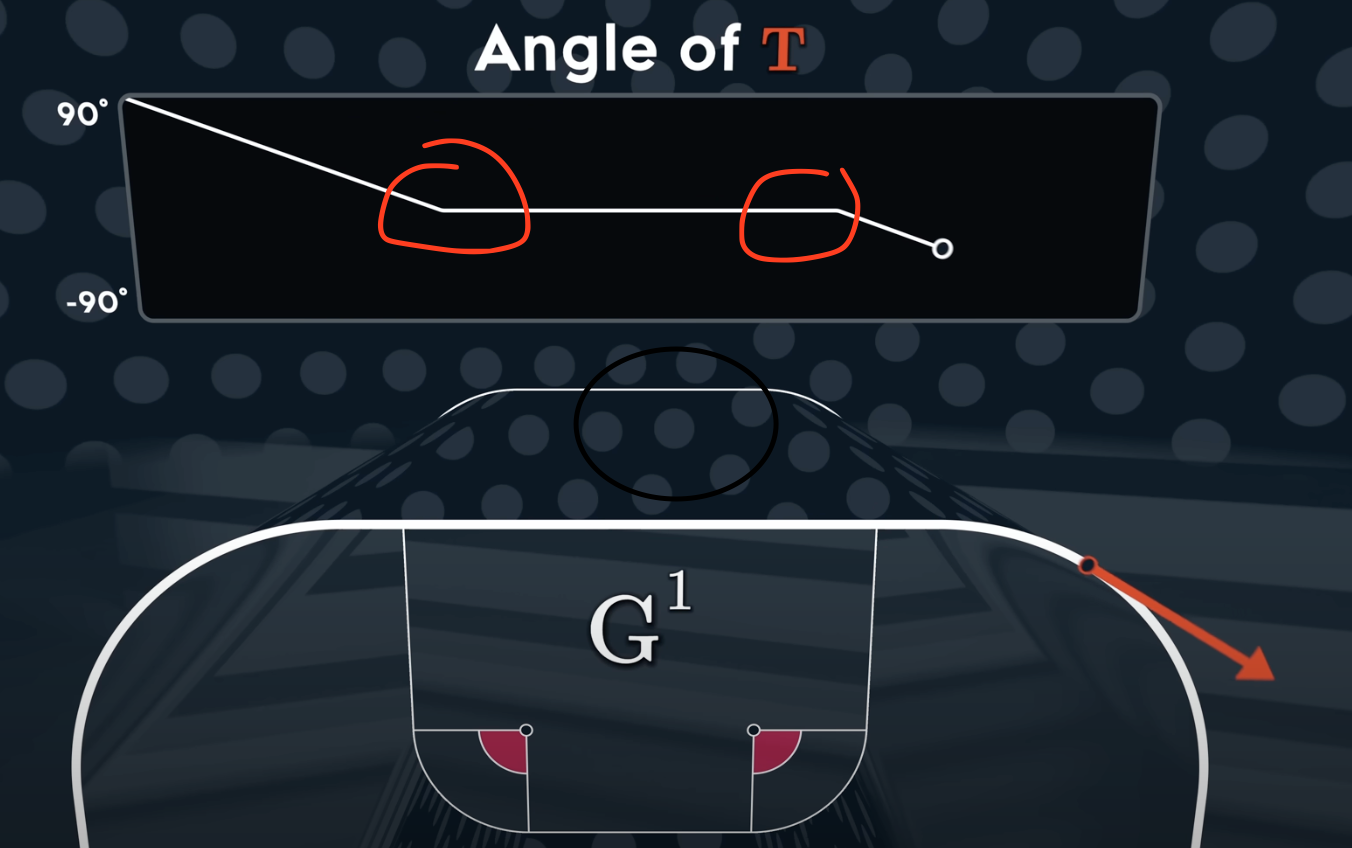
How about $G^2$? This is the continuity of the reflections!!!
Even the circle surface is NOT $G^2$
Why? The norm direction of the curve have a non smooth change
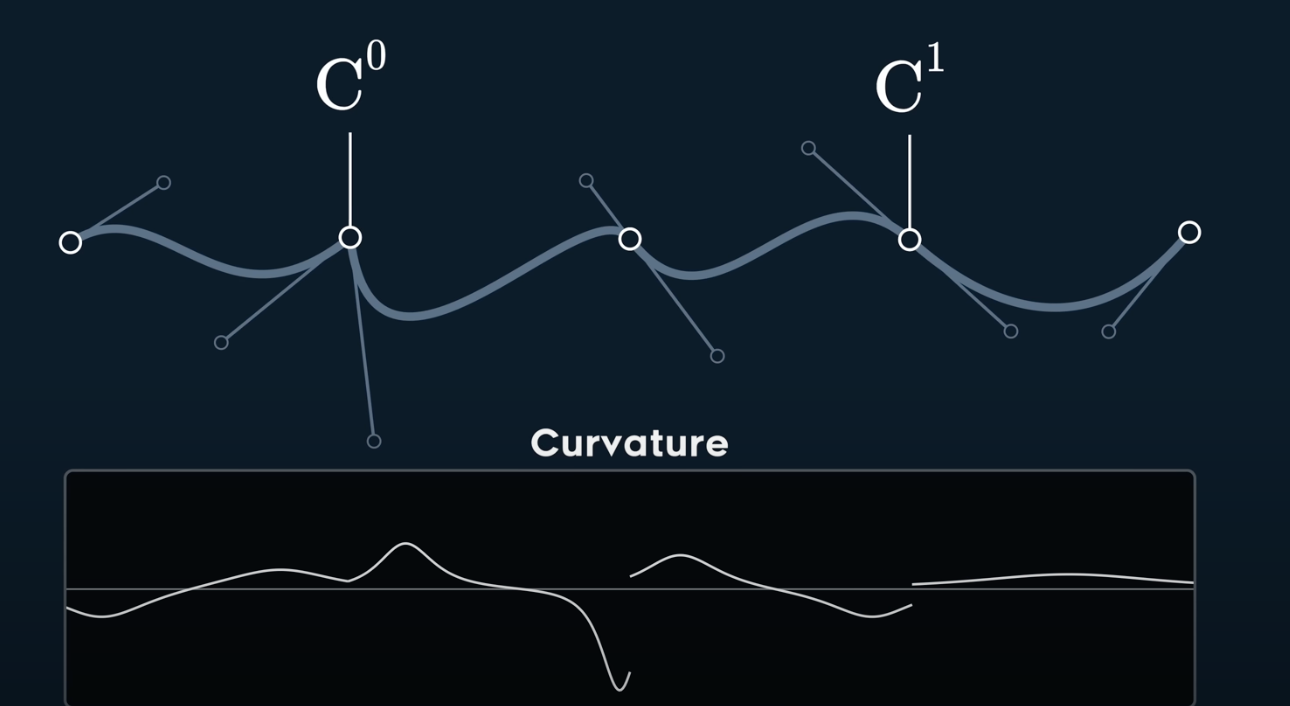
4 Curvature
Curvature is defined as below
and the relation between continuity and curvature is tricky
- $C^0$ may have continuous curvature
- $C^1$ does NOT guarantee the
continuous curvature
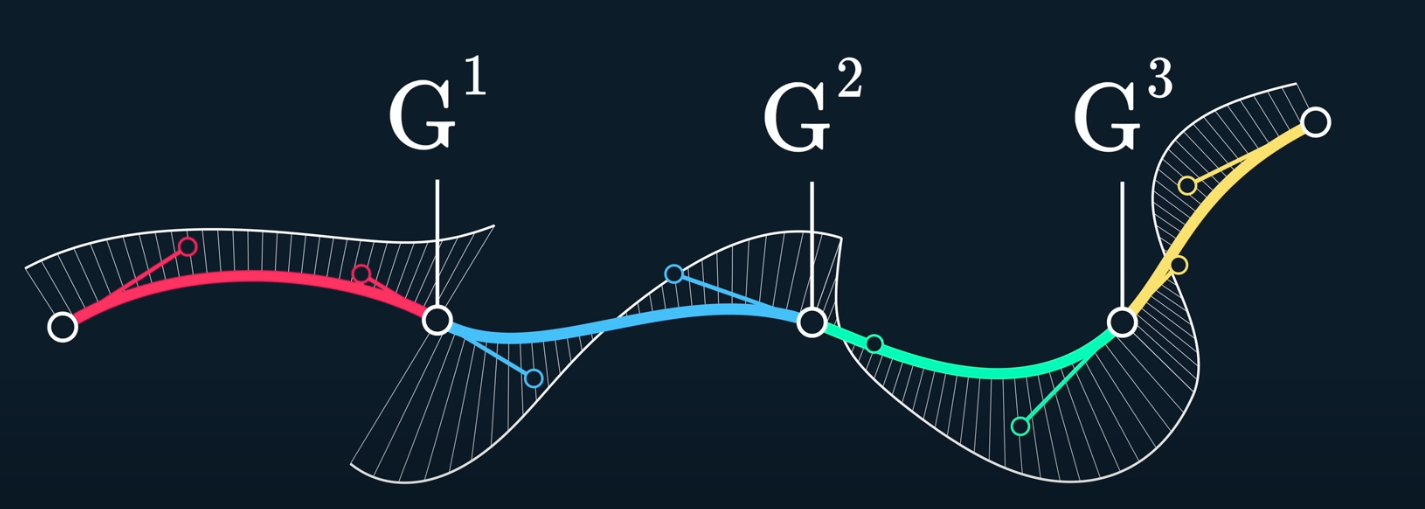
So we can understand GC as below
- $G^1$ is aligned curvature
- $G^2$ is continuous curvature
- $G^3$ is $C^1$ in curvature comb
or the official defination of GC is below.
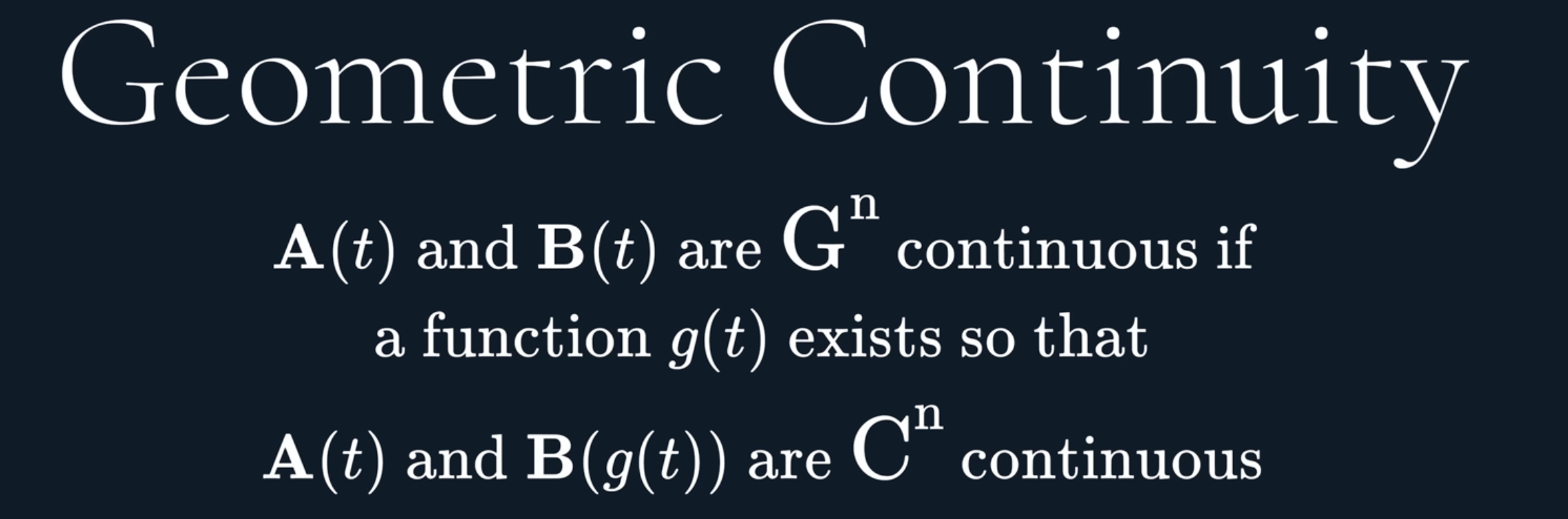and it’s related to Parametric Continuity as below
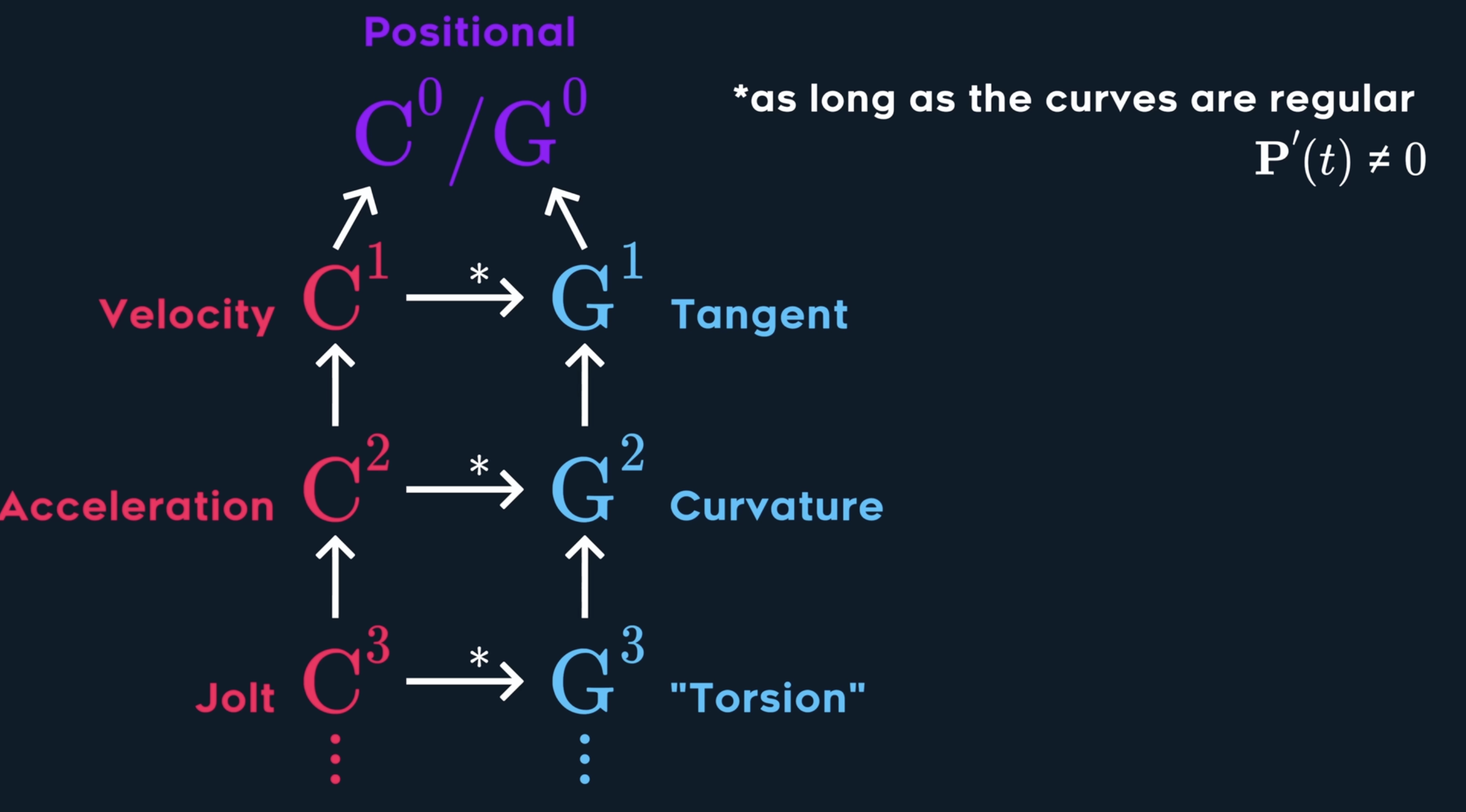
Now you can see the reflection is connnected on $G^2$ surfaces.
