Entropy and Perplexity

Understanding Shannon’s entropy is curcial to understand concepts like cross entropy and KL divergenece. But perplexity is the concept comes with NLP. Here is a good intuition explanation here and here on medium.

1 Why $\frac{1}{p(x)}$ the amount of information.

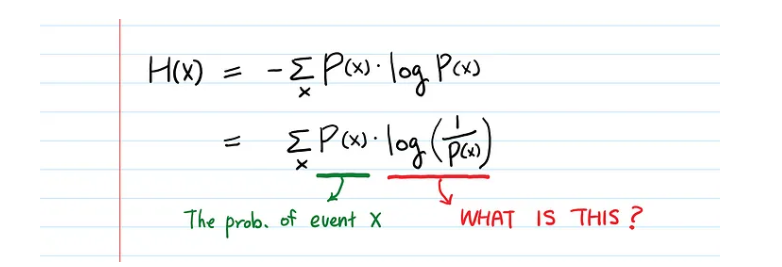For equally likely events, exclusive with prop. $p$, knowing one event means knowing the results of all the others, so the total information is $1/p$. For examples, if we know Nazis lose, then we know US, UK and China won separetly, total 4 events ( 1 / 25%)
For NOT equally likely events, like now US, UK and China are allies, any of them won means Nasiz lose, then Nazis can win w a chance of 25%. If it happens, the information contains in it is same as the previous case.

When any of the allies won, we know Nazis lost, but only 1/3 of Nazis lose event. This is the tricky part, even though Nazis lose is a fact when any of the allies won, but still considier 1/3 of the event, so that all allies won, can make the Nazie lose a whole event. So the information get from one ally win, is 1 plus 1/3.

Then is the rest of the Entropy forumula is straightforward as the expected value of every possible information.

2 Why take the $log$

Entropy is the defination of uncertainty and need to start thininig in terms of the “bits”.

2 status events can be presented by 1 bit, 1 or 0. and 4 status events can be expressed as 00, 01, 10 and 11. So the $log$ operation is to get the “amount of information” contained in the variable.

Putting everything together we get the defination of Entropy, which is average number of bits that we need to encode the information.

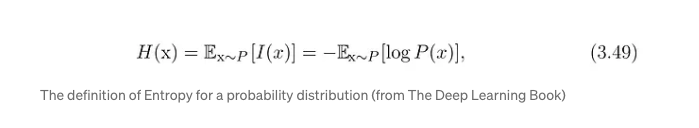
3 Perplexity

In general, perplexity is a measurement of how well a probability model predicts a sample. Mathmatically, perplexity is just an exponentiation of the entropy. Less uncertain, the smaller perplexity, and the better!

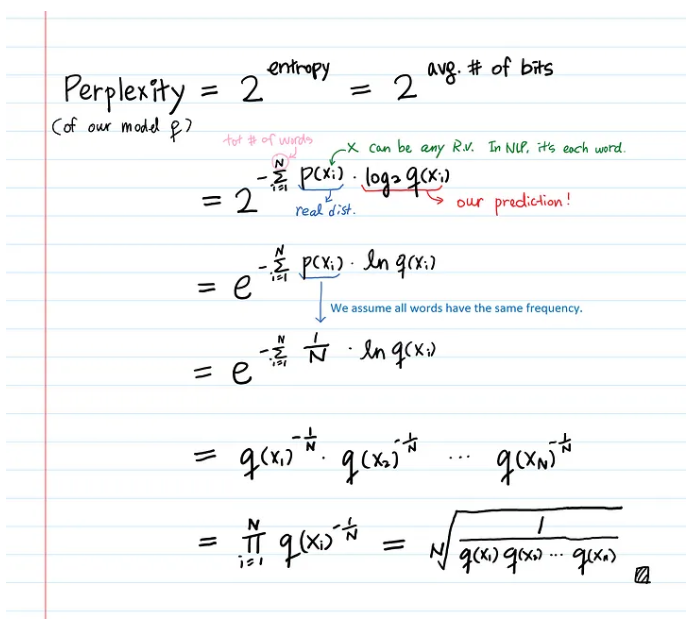
Pay attention here $p$ is the prob. distrition we want to model.Training sample is drawn from $p$ and it’s distribution is unknow.

$q$ is a proposed model, which is our prediciton.

When evaluate our prediction $q$ by testing against samples drawn from $p$, it’s essencially calculate the cross-entropy.

Now, this Perplexity deck is more easy to digest now.