Kolmogorov-Arnold Network
It’s all over the internet about how KAN will revolutionize ML by replacing MLP. Here are my frist read about KAN
0 Motivations and Spline
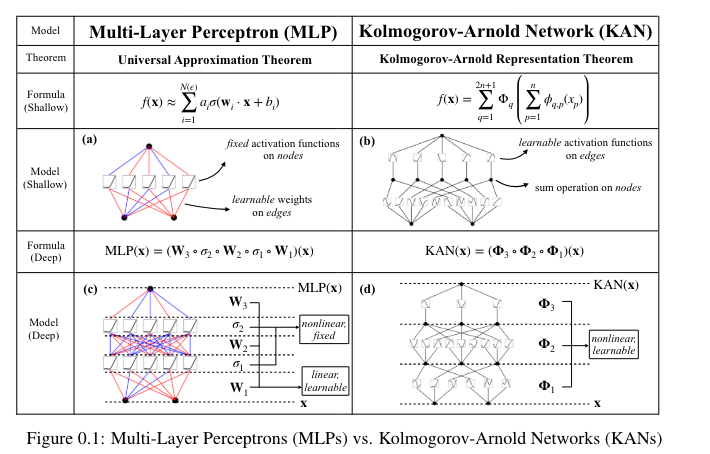
While MLPs have fixed activation functions on nodes (“neurons”), KANs have learnable
activation functions on edges (“weights”). KANs have NO linear weights AT ALL – every
weight parameter is replaced by a univariate function parametrized as a spline.
A spline is a function defined piecewise by polynomials. For example cubic spline is defined by 3rd order polynoimals in each segment $[t_{i-1}, t_i], i=1…n$

In order to solve this equation with $4n$ parameters, we already have $3(n-1)$ equations shown above.
By constraining $S(x_i)=y_i, i=0…n$ gives another $n+1$ equations.
The last two constrains can have different options, and by setting $S(t_0)=S(t_n)=0$ gives you natural cubic spline
1 Kolmogorov-Arnold Representation theorem
Vladimir Arnold and Andrey Kolmogorov established that if $f$ is a multivariate continuous function on a bounded domain, then $f$ can be written as a finite composition of continuous functions of a single variable (univariate) and the binary operation of addition.

2 Kolmogorov-Arnold Network (KAN)

With this generalization of $\Phi$, then KAN can be constructed simply by stacking layers!
\(KAN(X)=\Phi_{L-1}\circ...\circ\Phi_1\circ\Phi_0\circ X\)
In constrast, a MLP is interleaved by linear layers $W$ and nonlinearities $\sigma$: \(MLP(X)=W_{L-1}\circ\sigma\circ...\circ W_1\circ\sigma\circ W_0\circ\sigma\circ X\)