Andrej Karpathy-Backprop

Andrej explain his own blog in this lecture.

1 Gradients

• Basic operatinos w Chain Rule

  # batch_size 32, embed_size 27
  #logprobs.shape = [32, 27] 
  #loss = -logprobs[range(n), Yb].mean()
  dlogprobs = torch.zeros_like(logprobs)
  dlogprobs[range(n), Yb] = -1.0/n
  #logprobs = probs.log()
  dprobs = (1.0 / probs) * dlogprobs
  

• Sum over all grad contributions

  # counts.shape = [32, 27]
  # counts_sum_inv.shape == [32, 1]
  # dprobs.shape = [32, 27]
  #probs = counts * counts_sum_inv
  dcounts_sum_inv = (counts * dprobs).sum(1, keepdim=True) # The SUM!!!
  dcounts = counts_sum_inv * dprobs
  

• Use power -1 instead of reciprocal

  # counts_sum.shape == [32, 1]
  #counts_sum_inv = counts_sum**-1
  dcounts_sum = (-counts_sum**-2) * dcounts_sum_inv
      
  

• Addition is simply a route for grads.

  #counts_sum = counts.sum(1, keepdims=True)
  # use += to add this update to dcounts
  dcounts += torch.ones_like(counts) * dcounts_sum
  

• .exp() is the simplest

  #counts = norm_logits.exp()
  dnorm_logits = (norm_logits.exp()) * dcounts
              = counts * dcounts
  

• Subtraction is also a route for grads but with a negative sign
  Since the subtraction here is only for numerical stability reason, so the dlogit_maxes should be zero and actually it is (very small values)

  # subtract max for numerical stability
  # logits.shape == [32, 27]
  # logit_maxes.shape == [32, 1]
  #norm_logits = logits - logit_maxes 
  dlogits = dnorm_logits.clone() #clone for satety
  dlogit_maxes = (-1*dnorm_logits).sum(1, keepdim=True)
  

• Max operra
  • max returns both value and indices
  • use F.one_shot to generate one shot vectors for the correct max positions

    # F.one_shot().shape == [32, 27]
    #logit_maxes = logits.max(1, keepdim=True).values
    dlogits += F.one_hot(logits.max(1).indices, num_classes=logits.shape[1]) * dlogit_maxes
    

• Matrix multiplication
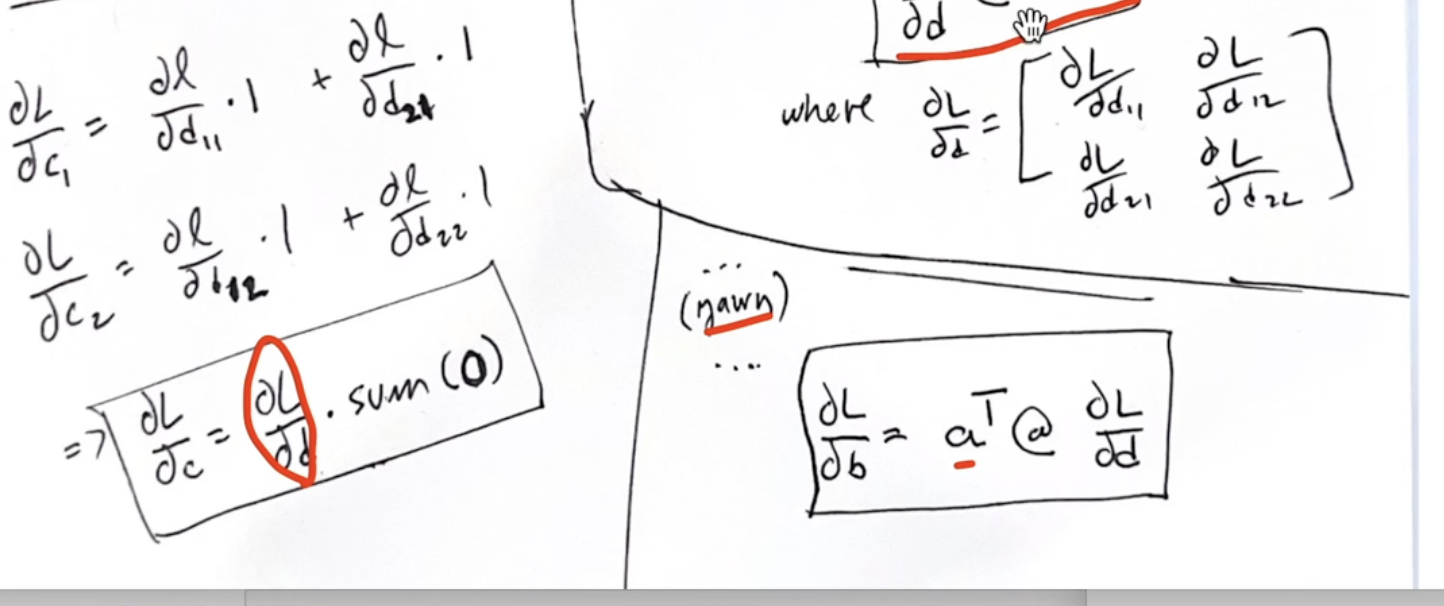  The trick here is the see how matrix dim can match.

  # logits.shape == [32, 27]
  # h.shape == [32, 64] W2.shape == [64, 27]
  # b2.shape == [27]
  # logits = h @ W2 + b2
  # [32,27] + [27] --> [32,27] + [32,27]
  dh = dlogits @ W2.T
  dW2 = h.T @ dlogits
  db2 = dlogits.sum(0, keepdim=False)
  

• Tanh

  # Non-linearity
  h = torch.tanh(hpreact) # hidden layer
  dhpreact = (1-h**2) * dh
  

• Bessel’correction for variance unbiased variance estimation by dividing n-1 Batches are just a small sample, so it’s suggets to use the unbiased estimation.

  # unbiased variance estimation
  #bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True)
  # bnvar.shape == [1,64]
  # bndiff2.shape == [32,64]
  dbndiff2 = (1/(n-1))*torch.ones_like(bndiff2)*dbnvar
  

  This is different from grads for sum(1) as we don’t sum over but simply do assignment

• concatenataion Simply revert to the original shape

  # embcat.shape == [32, 30]
  # emb.shape == [32, 3, 10]
  # embcat = emb.view(emb.shape[0], -1) 
  demb = dembcat.view(emb.shape)
  

• Indexing Also a re-route similar to concat, but need to find the correct indexing

  # emb.shape == [32, 3, 10]
  # C.shape == [27, 10]
  # Xb.shape == [32, 3]
  # emb = C[Xb]
  dC = torch.zeros_like(C)
  for k in range(Xb.shape[0]):
    for j in range(Xb.shape[1]):
      ix = Xb[k,j]
      dC[ix] += demb[k,j]
  

2 Simple solution for cross_entropy

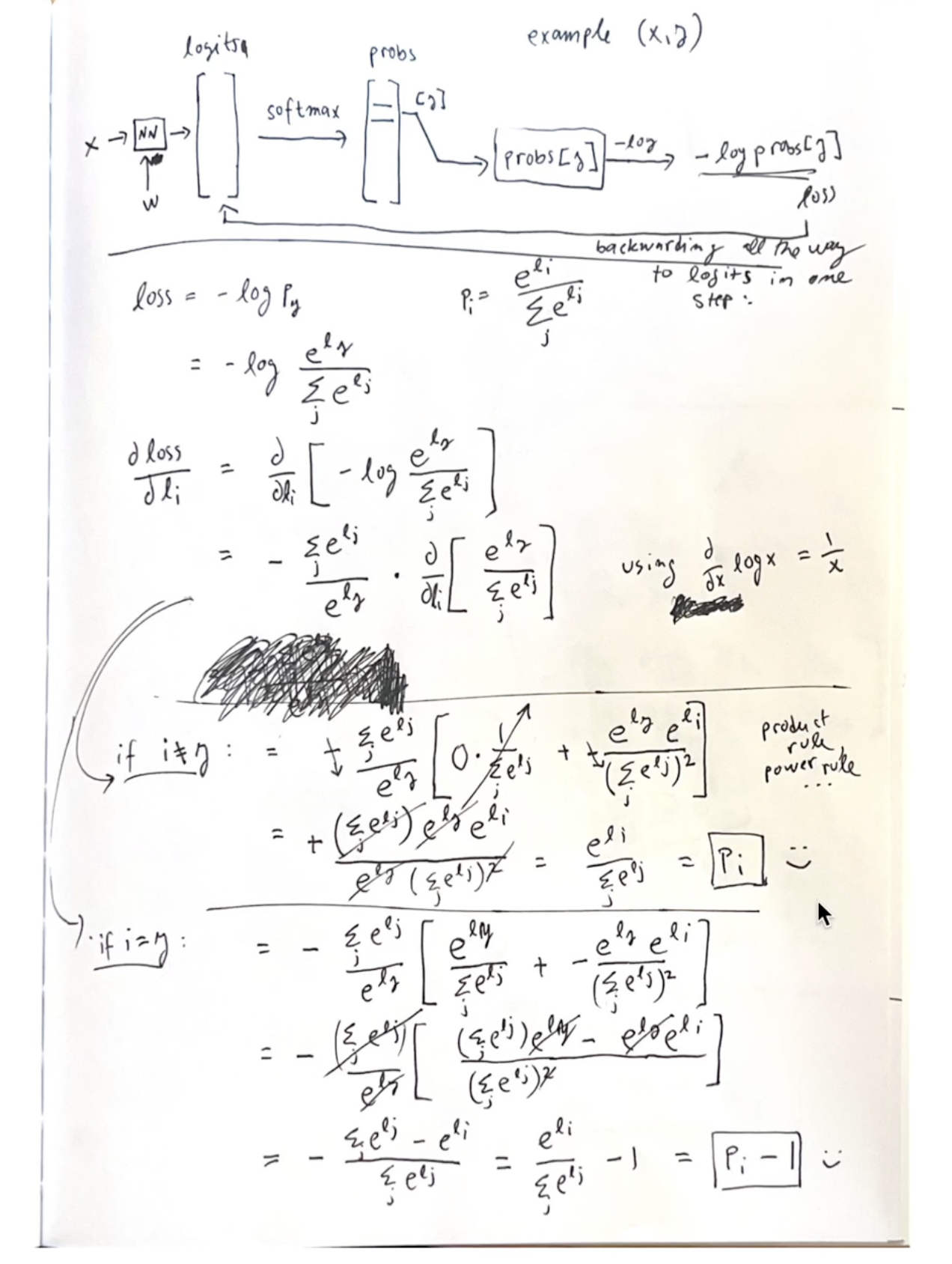
  #loss = F.cross_entropy(logits, Yb)
  dlogits = F.softmax(logits, 1)
  dlogits[range(n), Yb] -= 1
  dlogits /= n  

3 Simple solution for Batch Norm

Pretty tricky math here

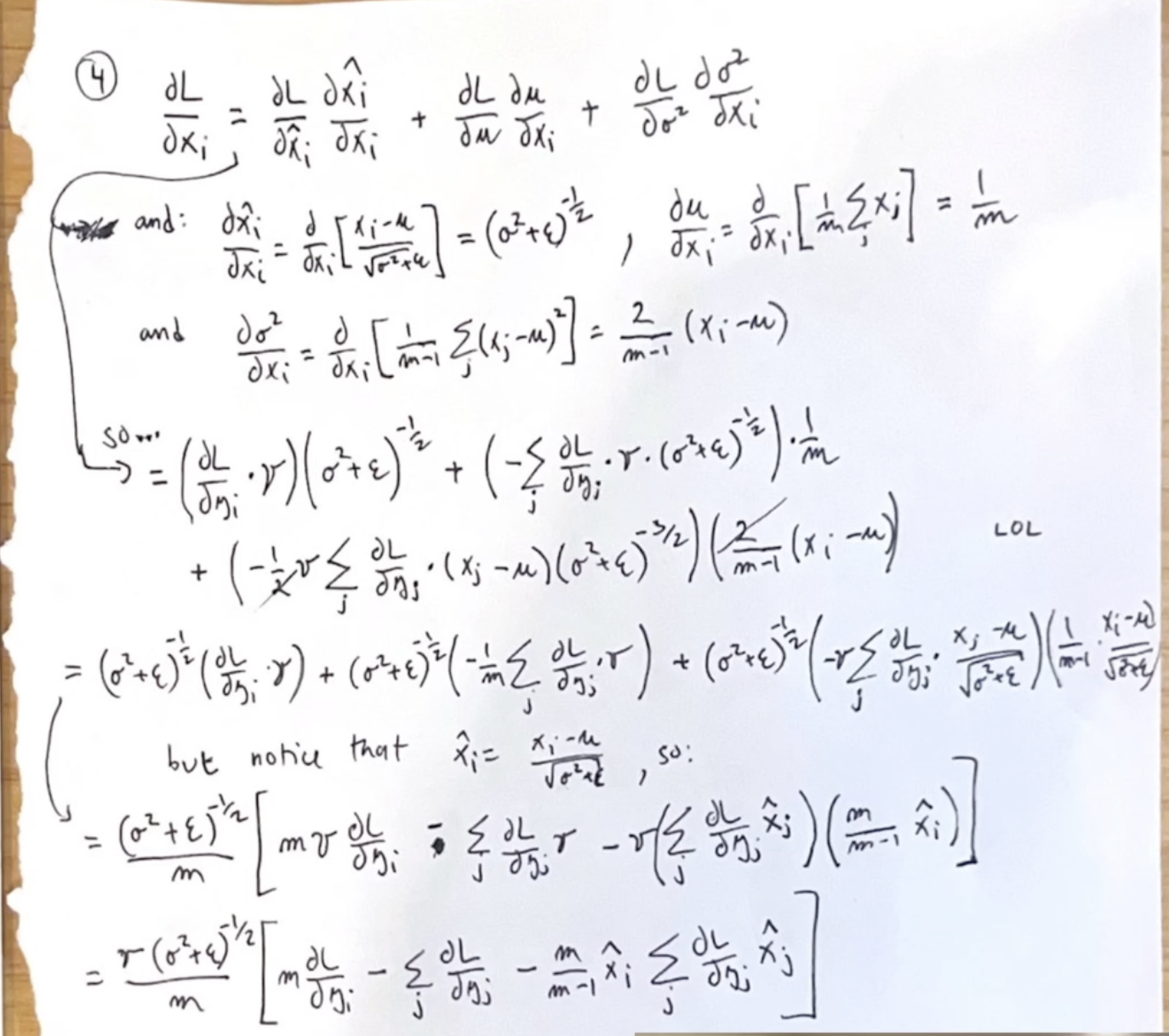
  #hpreact = bngain * (hprebn - hprebn.mean(0, keepdim=True)) / torch.sqrt(hprebn.var(0, keepdim=True, unbiased=True) + 1e-5) + bnbias

  dhprebn = bngain*bnvar_inv/n * (n*dhpreact - dhpreact.sum(0) - n/(n-1)*bnraw*(dhpreact*bnraw).sum(0))