Andrej Karpathy-BatchNorm

This part goes deep into some training tricks. Very insightful!

1 Fixing issues

• Fixing the inital loss
  To fix it, we can reduce the input into softmax. So we simply scale down the last layer’s weight and biases.

  W2 = torch.randn((n_hidden, vocab_size),          generator=g) * 0.01
  b2 = torch.randn(vocab_size,                      generator=g) * 0
  #logits = h @ W2 + b2 # output layer
  #probs = torch.softmax(logits, dim=0)
  

• Tanh Saturation
  • tanh can ONLY decrease the grad.
  • if input is too small, tanh can’t pass the grad ($1-t^2$ when t->0)
  • if input is too larger, tanh is saturated. ($1-t^2$ when t->1)

  hpreact is too far away from zero, so h is either -1 or 1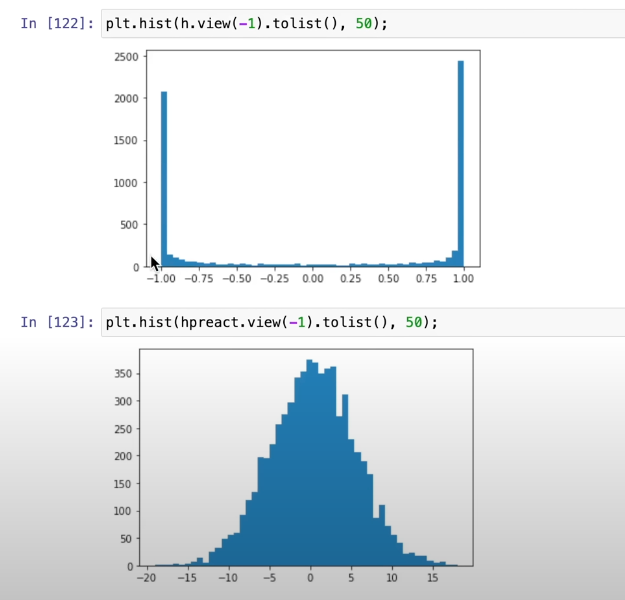

  # Reduce W1 and b1 to reduce hpreact
  W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) *0.2
  b1 = torch.randn(n_hidden,                        generator=g) * 0.01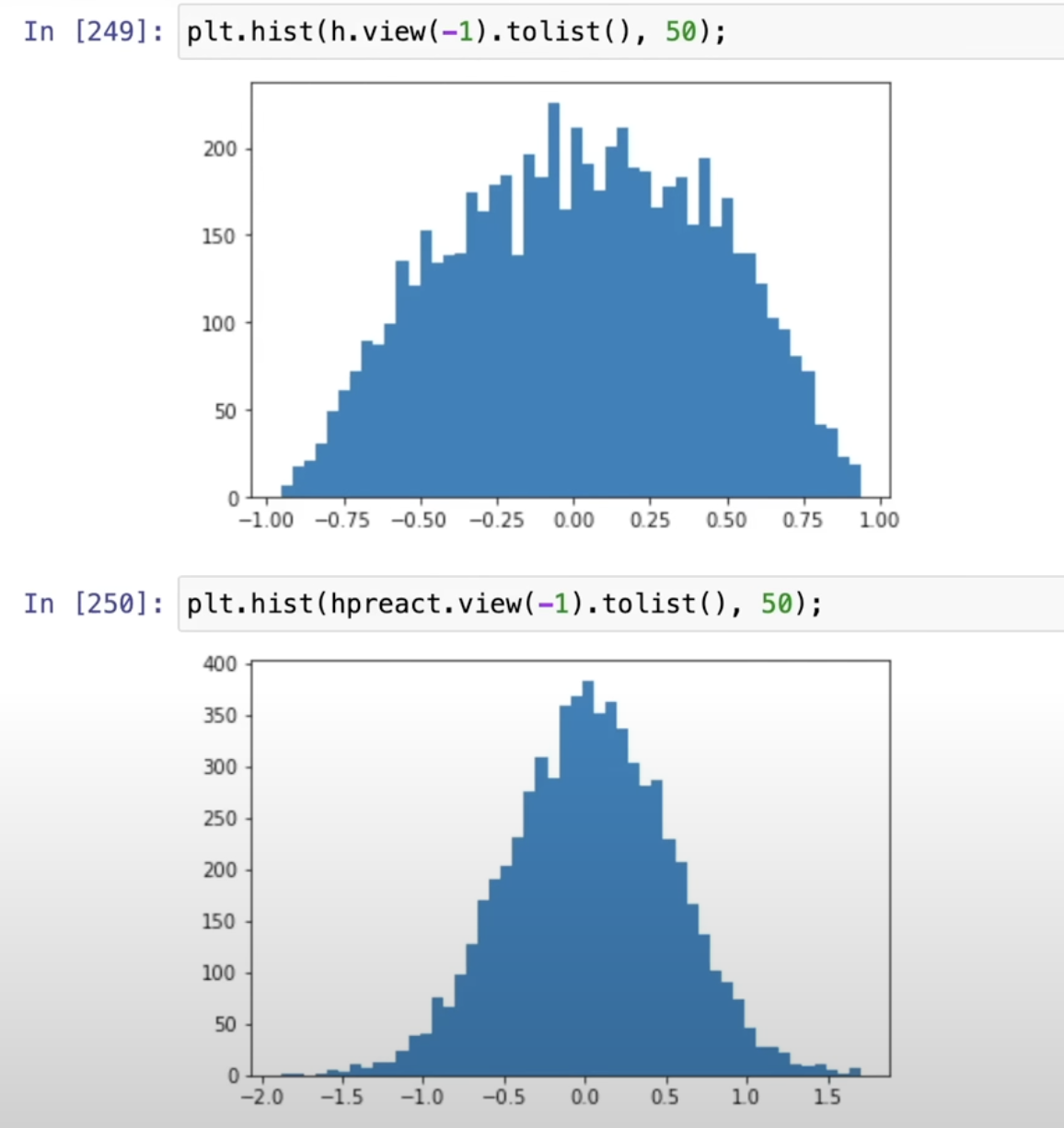
  

  Now the question is, how to get the 0.2 value?

• Kaiming Init
  The weight would change the std of input x. To keep std to be 1 at each layer, we can let
  $w *= 1/(fan_in)^{const}$
  This is from Kaiming’s paper and implemented in torch as torch::nn::init::kaiming_normal_ with a constant depends on the activiation function.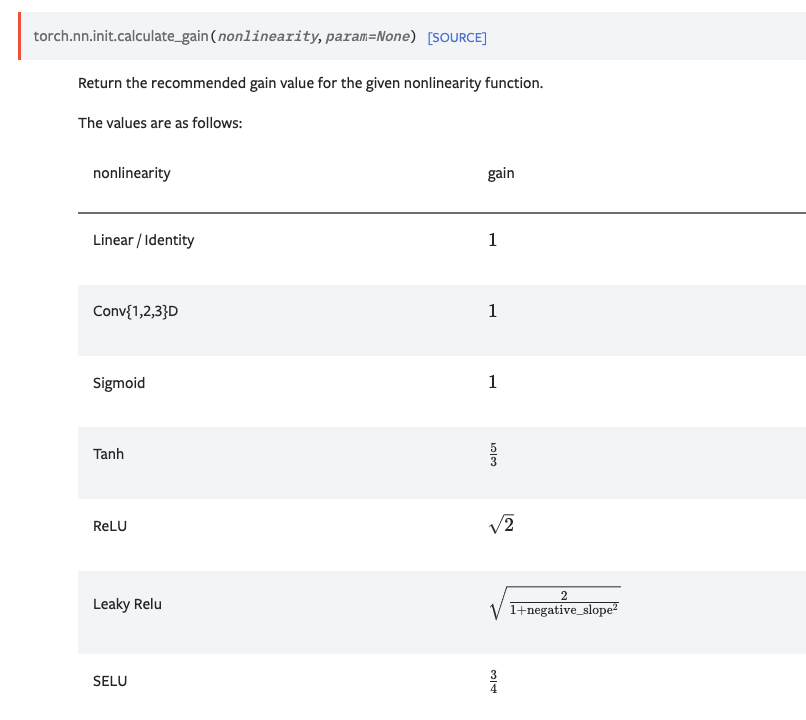 So the W1 should be inited as below:

  W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) * (5/3)/((n_embd * block_size)**0.5) 
  

  The weight is 0.3, so 0.2 is close enough.
  This step is less important after Batch/Layer Norm.

2 Batch Norm

Google published Batch norm paper. Both writers are in xAI now.

• Train time

  #bngain = torch.ones((1, n_hidden))
  #bnbias = torch.zeros((1, n_hidden))
  #bngain.requires_grad = True
  #bnbias.requires_grad = True
  # This 0 dim in mean/std is the batch dim!
  bnmeani = hpreact.mean(0, keepdim=True)
  bnstdi = hpreact.std(0, keepdim=True)
  hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
  

• Inference time The mean/std used in inference time is from Training data in two ways.
  • Use the total mean and std of the training dataset

    with torch.no_grad():
      # pass the training set through
      emb = C[Xtr]
      embcat = emb.view(emb.shape[0], -1)
      hpreact = embcat @ W1 # + b1
      # measure the mean/std over the entire training set
      bnmean = hpreact.mean(0, keepdim=True)
      bnstd = hpreact.std(0, keepdim=True)
    
    

  • Calc the running mean/std of the training data

    with torch.no_grad():
      bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
      bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi
    

• Couple of points
  • Add $\epsilon$ to avoid div by zero
  • The bias before BN is wasteful, so should be removed.
  • The momentum for BN is the 0.001 for bnmean/std_running, and track_runing_stats is the flag for it in PyTorch
  • affine flag is for bngain/bias,which is trainable
  • GroupNorm and LayerNorm are more commonly used nowadays.
  • Need to carefully select initial weight, like Kaiming init with 5/3 scaler, without BatchNorm.
  • BatchNorm makes the initialization much less sensative.