Legendre polynomials and HiPPO

Study notes from the video presented by Albert Gu on S4, Structured State Space Sequence model

0 References

HiPPO: Recurrent Memory with Optimal Polynomial Projections paper by Albert Gu, Tri Dao, 2020

S4: Efficiently Modeling Long Sequences with Structured State Spaces paper by Albert Gu, 2021

Hungry Hungry HiPPO:Towards Language Modeling with State Space Models paper by Dan Fu, Tri Dao, 2022

The next one will discuss about Mamba: Linear-Time Sequence Modeling with Selective State Spaces paper by Albert Gu, Tri Dao, 2023

1 Legendre Polynomials

Legendre Polynomial is a set of orthogonal polynomials. They are solutions to Legendre DE
\((1-x^2)P{''}_n(x)-2xP{'}_n(x)+n(n+1)P_n(x)=0\) and can be rewrtie as following \(\frac{d}{dx}[(1-x^2)\frac{d}{dx}P(x)]+n(n+1)P(x)=0\)

• They are orthogonal on the interval [-1, 1] with respect to the uniform measure on that interval.
• Let $P_n$ be the nth Legendre polynomial. Then, for all n, $P_n(1)=1$ and $P_n(-1)=(-1)^n$
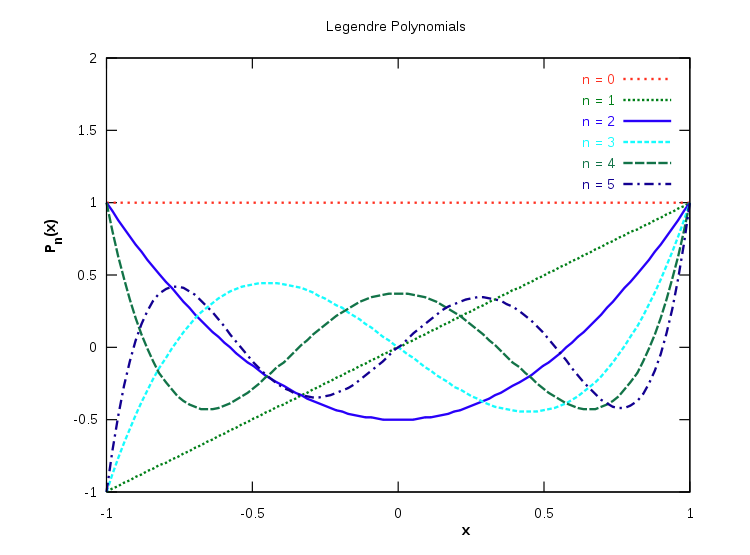
• You can also get LP recursively \((n+1)P_{n+1}(x)=(2n+1)xP_n(x)-nP_{n-1}(x)\)

  2 Exponential Moving Average

  Simply Moving Average is unweighted mean of the previous K data point in finance, or take equal number of data on either side of a central value in engineer and science.

Exponential Moving Average is weighted mean with a parameter $\alpha$. For new value $p_t$ at time $t$, we have
\(EMA_t = \alpha * p_t + (1-\alpha)*EMA_{t-1}\)

Plug in $EMA_{t-1}$ and so on, you will get
\(EMA_t = \alpha * (p_t + (1-\alpha)*p_{t-1}+(1-\alpha)^2p_{t-2}+(1-\alpha)^3p_{t-3}+...)\)

Here is the figure of EMA weights

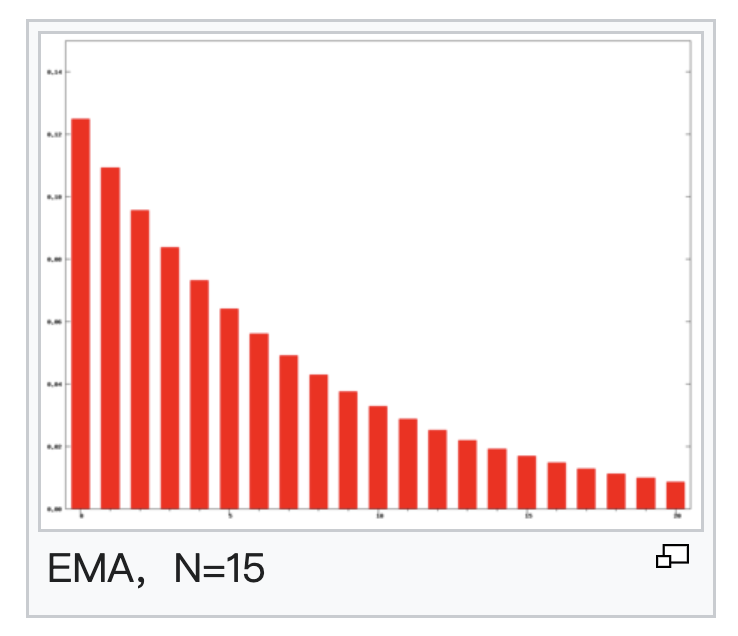
EMA can NOT be easily learnt due to unbouned context.

3 HiPPO

The problem HiPPO trying to solve is online memorilization: the long term memory issue and need to be updated in a constant time.

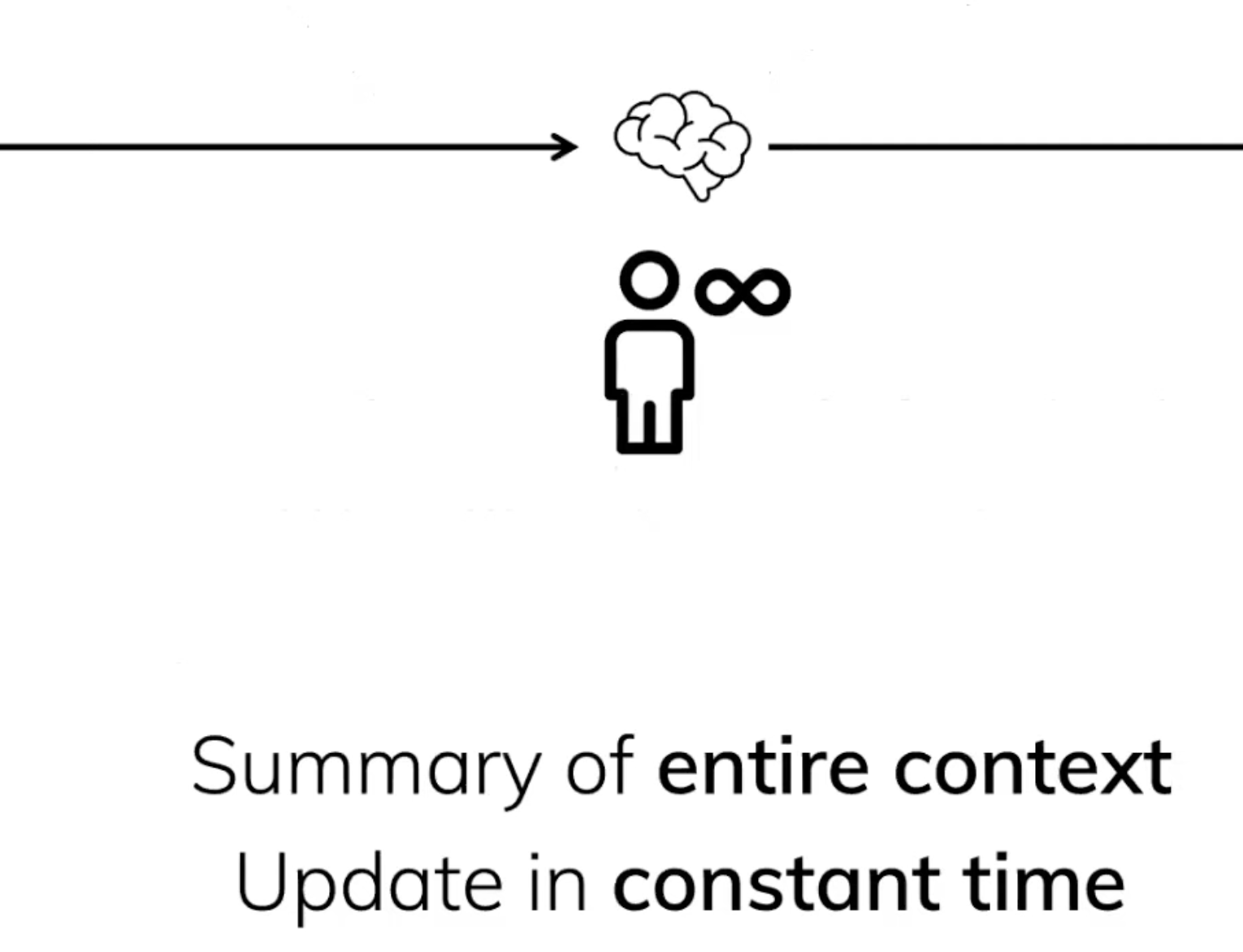
The solution is to use a polynomial to match the signal up to time $t$. The memory budge decides the polynomial degree.

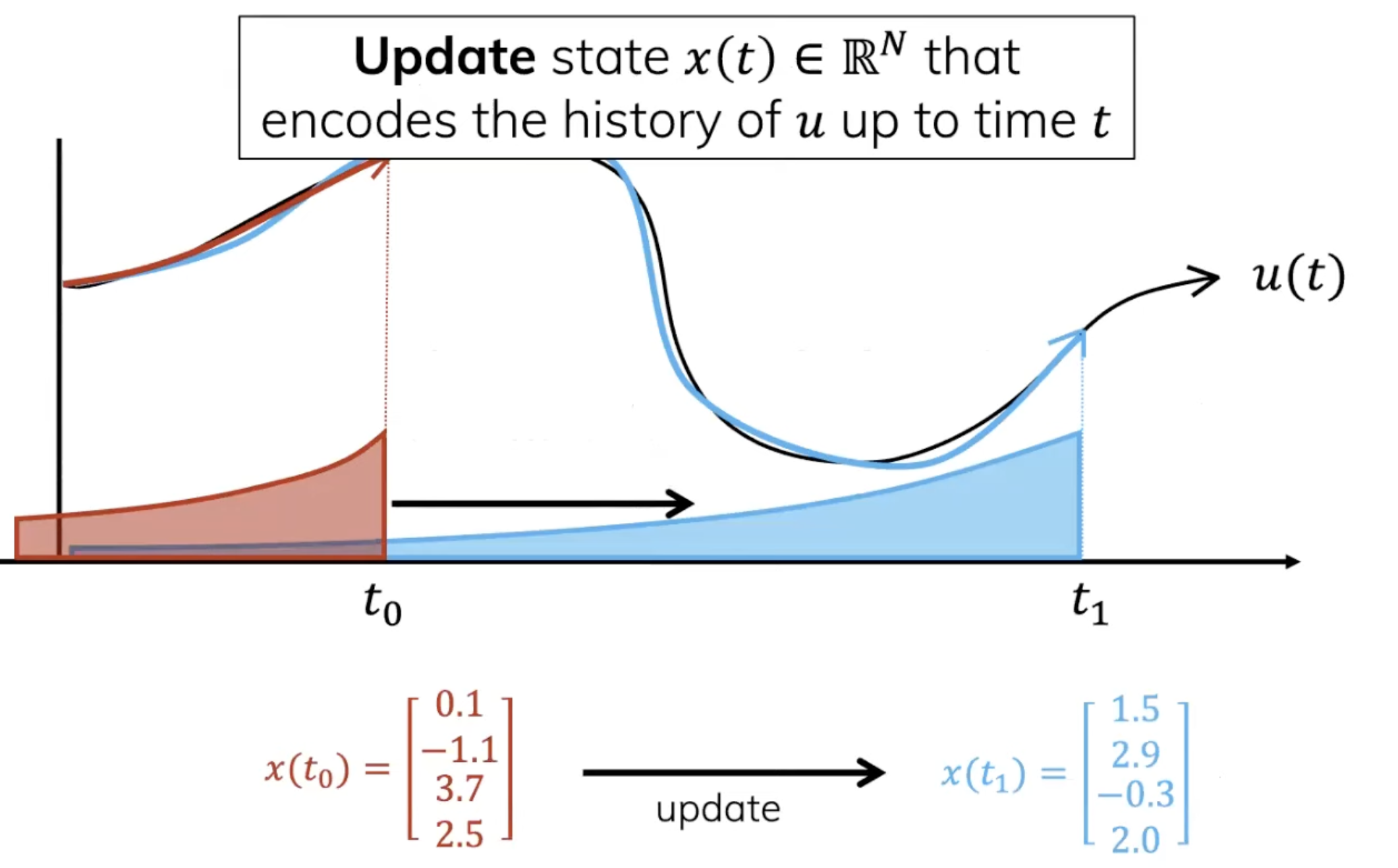
The difference of fitted polynomial and original singnal can be measured in different ways, like EMA.

HiPPO stands for High-Order Polynomial Projection Operator, and it has PDE operator and matrix defined as 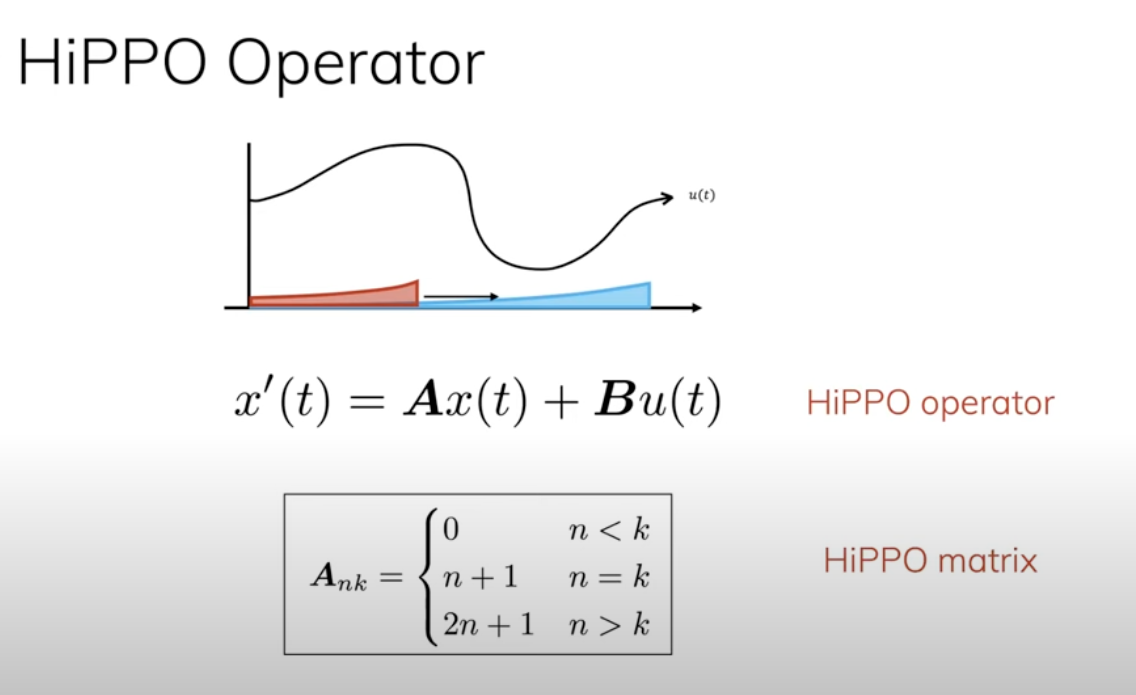The matrix essentially is
\(\begin{bmatrix} 1&0&0&0 \\ 1&2&0&0 \\ 1&3&3&0 \\ 1&3&5&4 \end{bmatrix}\)

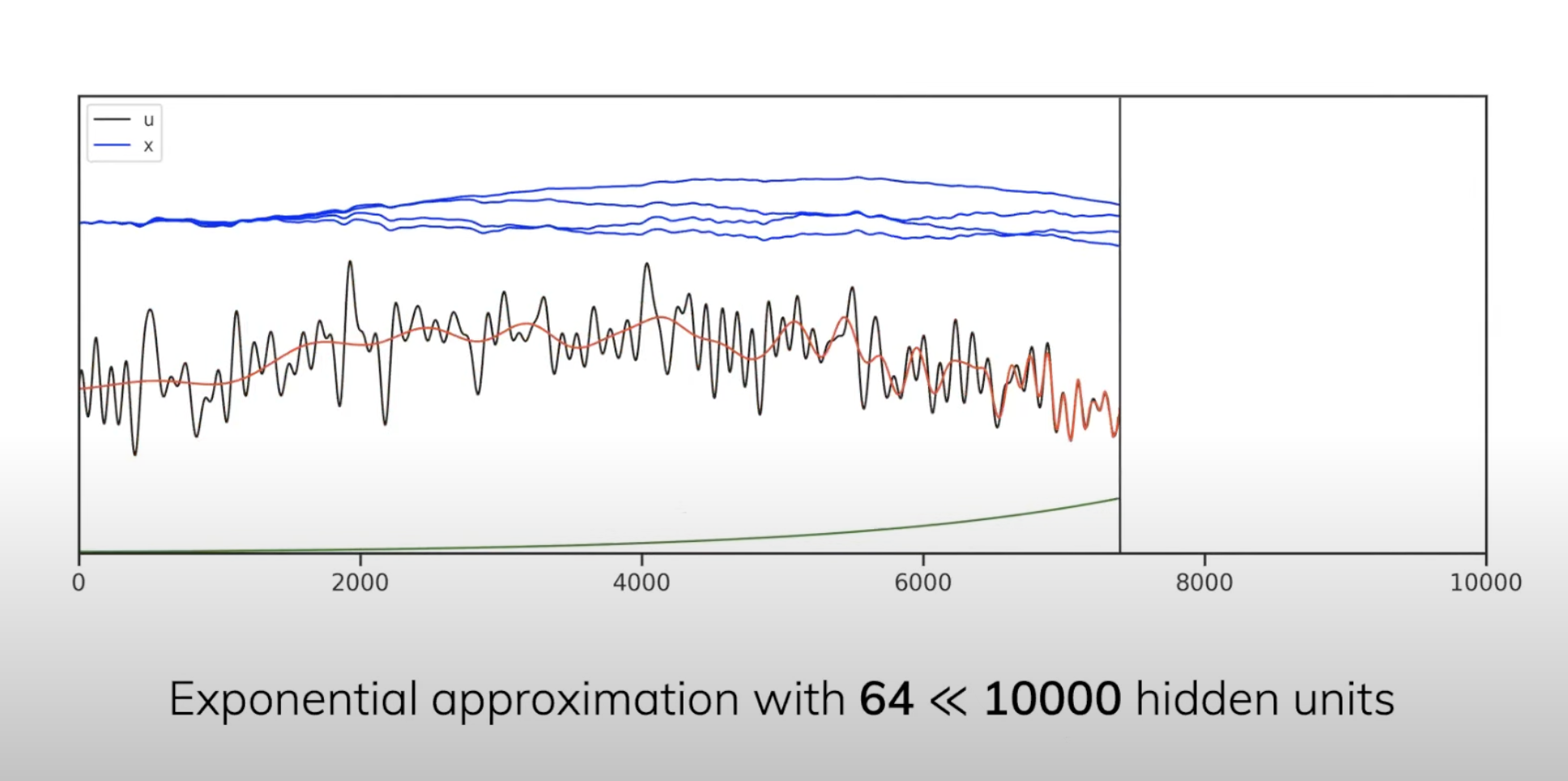
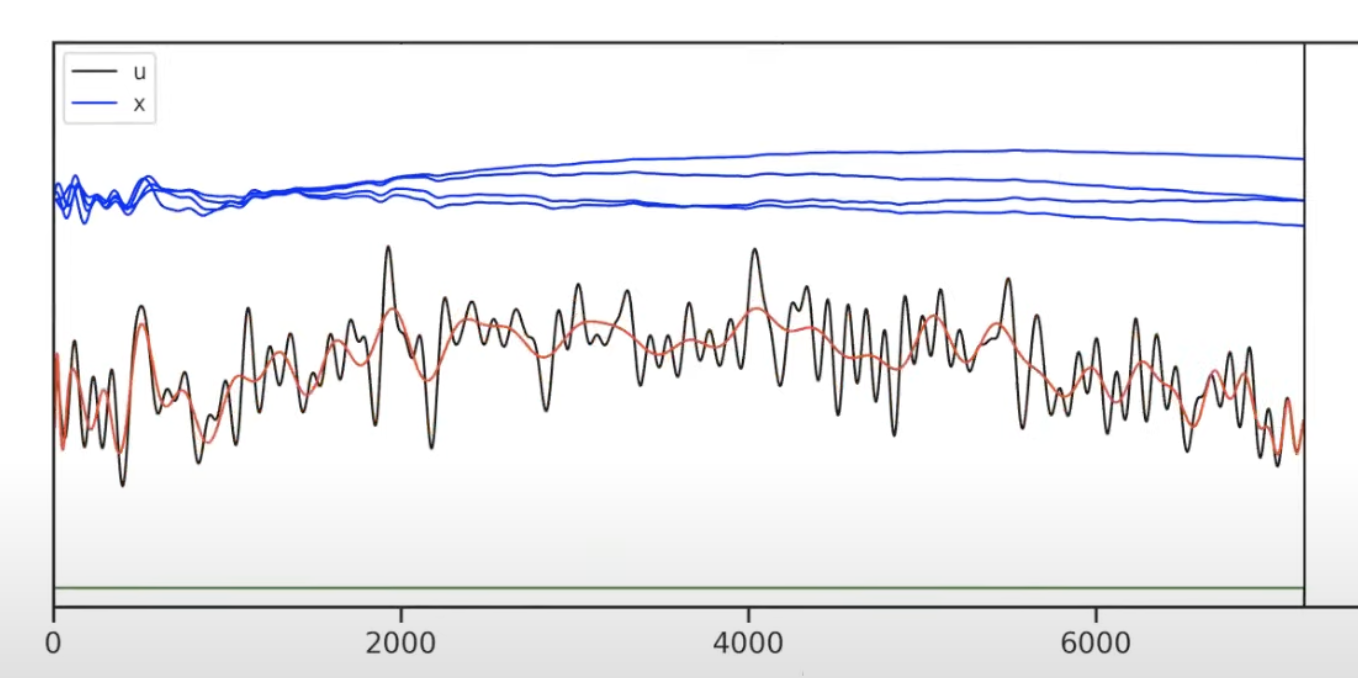
The coefficient X is actually 64 dim, and only showes 4 in the figure below. The latest X value represents the whole red curve which matches well in near and degrade in the past, which is exactly the EMA measure(green line).

You can also have uniform measure 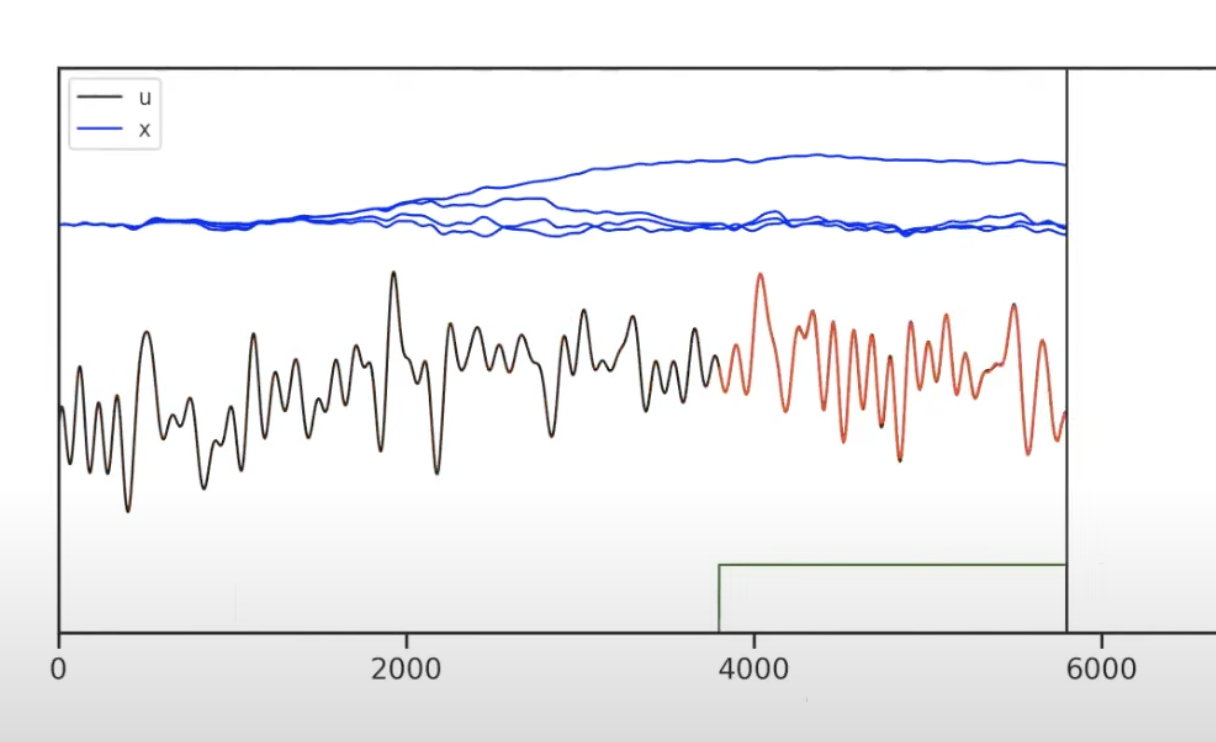or time-varying measure (see how the measure changes in these 2 figurs below)

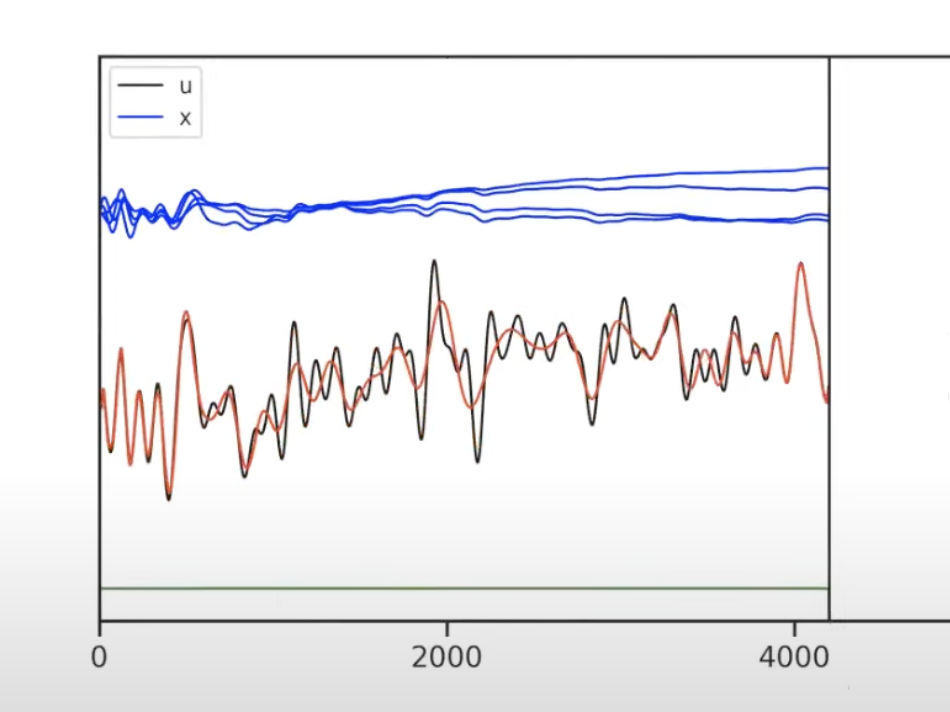
So the HiPPO can be generalized to
and the updates can be done in linear time ( what’s rank <3 ??)