ML101 -1
I was recommending some online materials for ML101 to a friend, and videos from Hung-yi Lee are always my first choices. I selected ML courses from his 2021 lessons and the first two covers the basics of ML
I learned similiar ML basis back in 2016, from coursera Machine Learning course, taught by Dr. Andrew Ng. Of couse, Who is not? It has been serveral years, so I dragged the playbar to check out how Dr Lee talked about basis and actually found sth quite inspiring. He is explaining things from a very different angle than Dr Ng, and looks so freshing.
So here we are, some notes from his basis talks
1, Sigmoid is used to simulate discrete step functions, which are used to create any continuous functions.
This is the first thing caught my eyes. Using activation functions in NN was always explained as introduing non-linearity, otherwise no matter how deep the NN is, is always a linear calculation as matrix multiplication. Dr Lee’s explaination is very straight forward, we need to fit a random continous function(red line), then we can consider it as a sum of multiple “step functions” like following blue lines. and the blue lines are actually can be simulated by sigmoid.
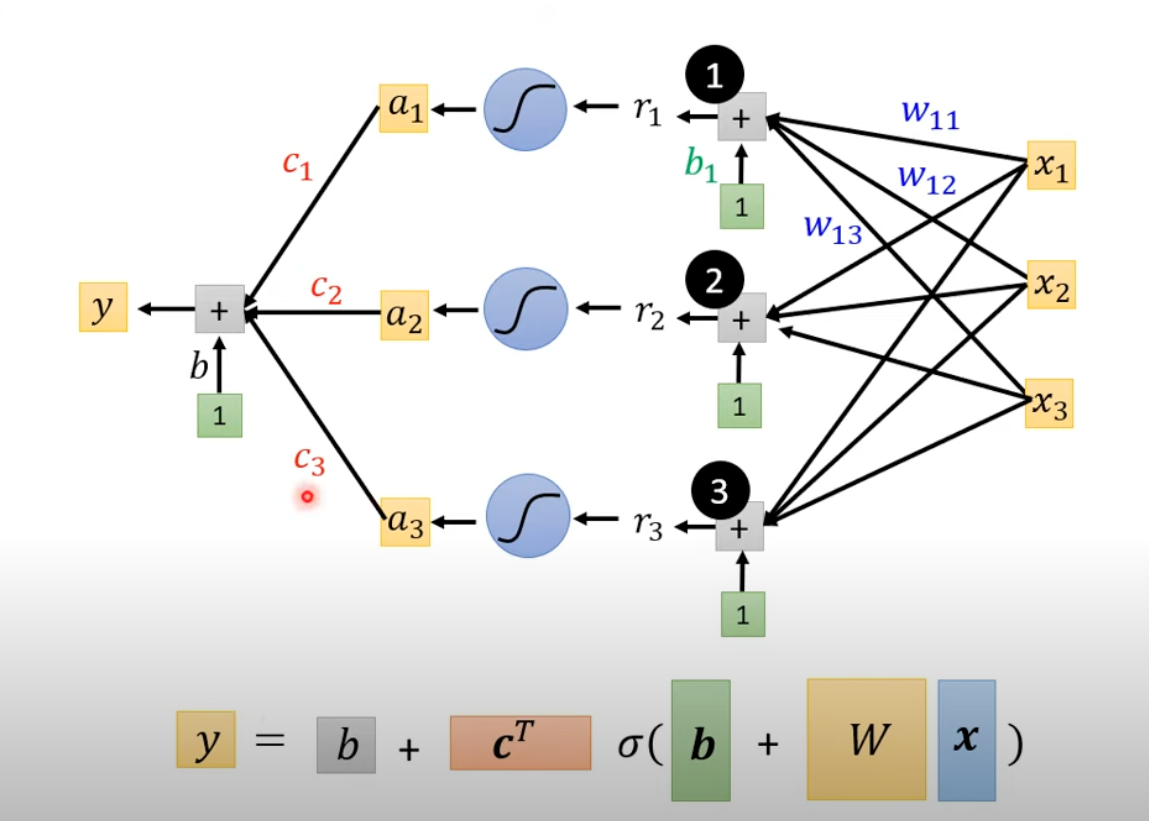
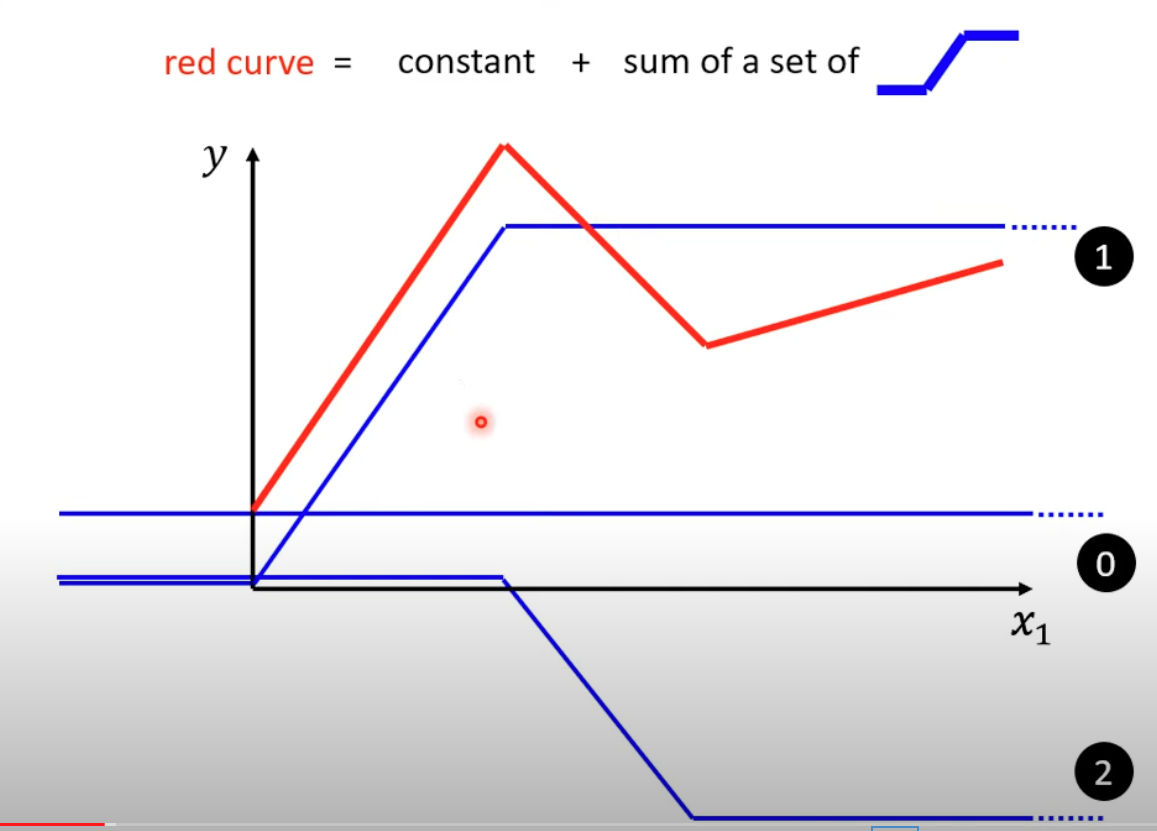Mathematically, when we sum up these sigmoid functions, it natureally becomes a 2 layer NN! Beautify!
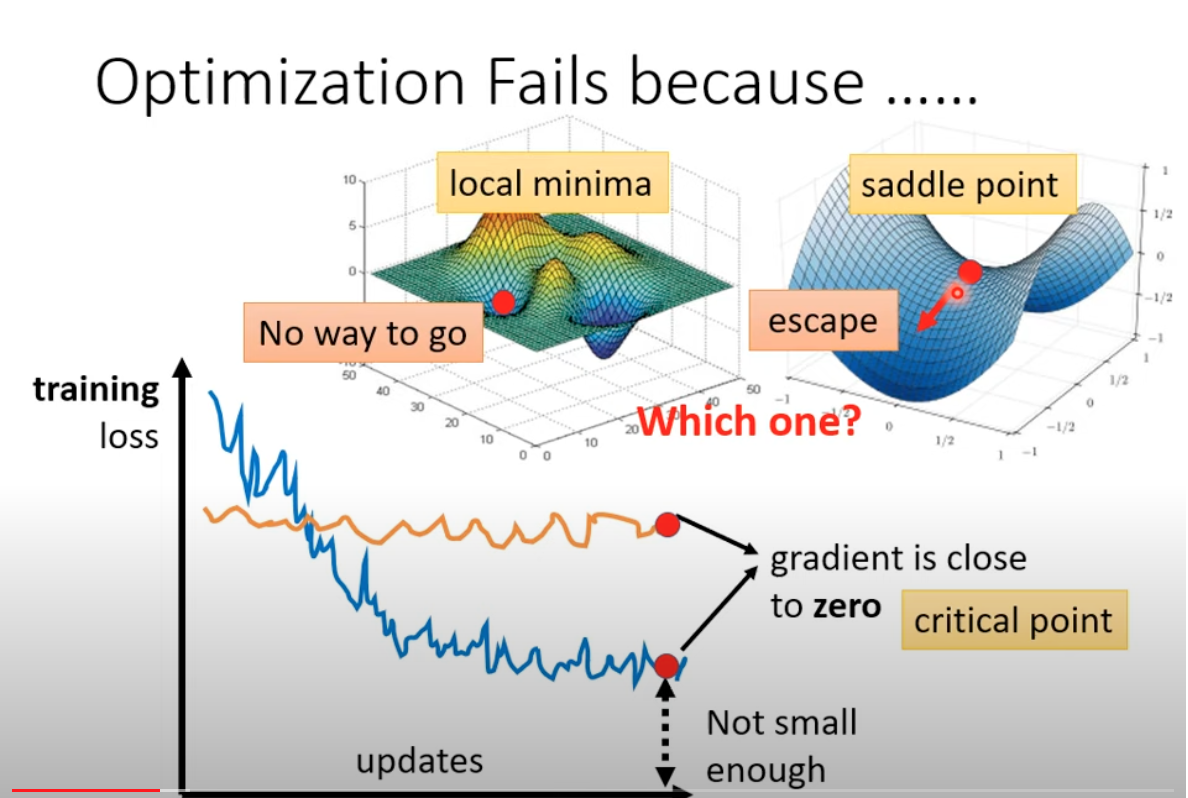
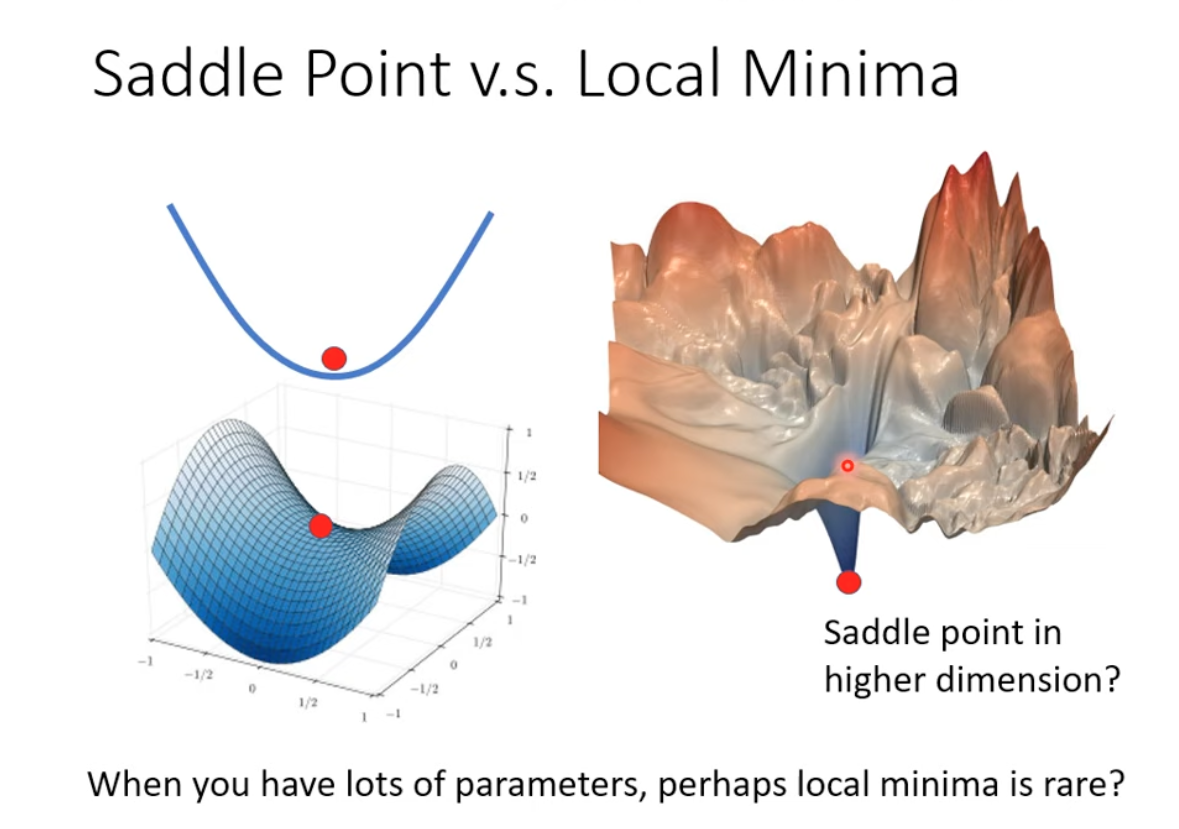
2 Local minimum VS Saddle point
The defination of these two are straight forward, and both are reasons of gradient vanishing. We can escape from the saddle point, which is better to handel than local min.
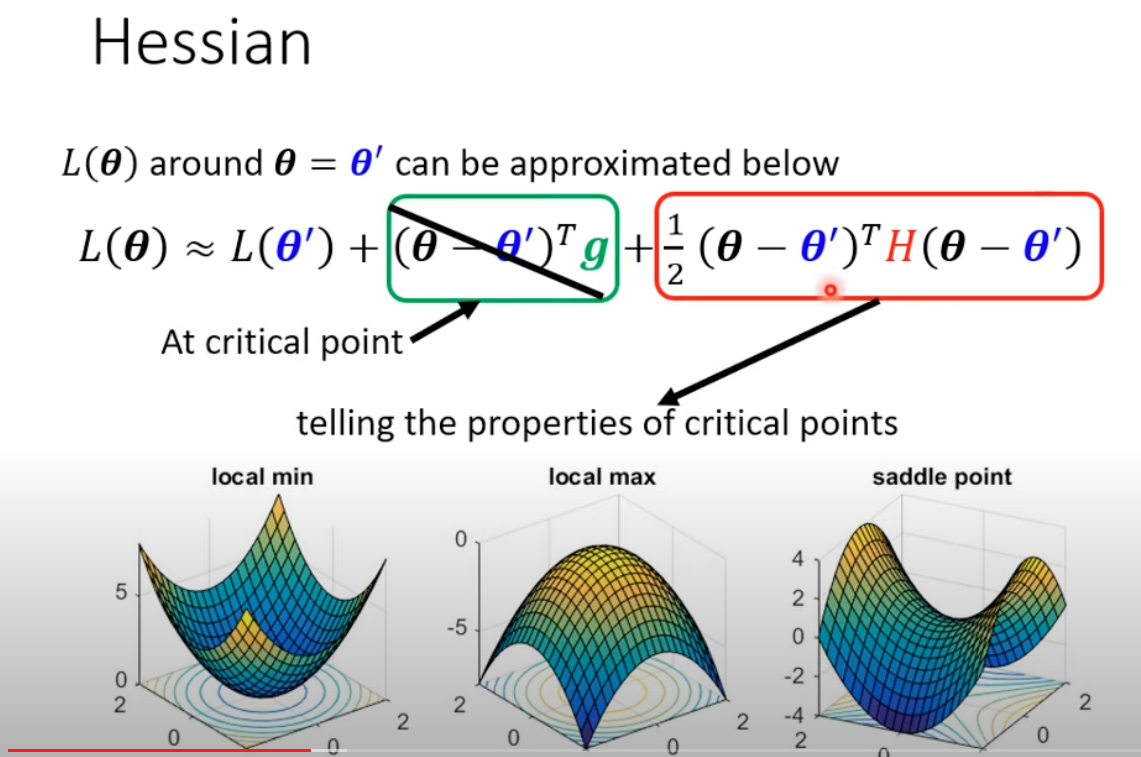
Dr Lee further did some math conduction to show the different of these two are to see if the Hession Matrix of the loss function are positive definite (all eigen values are positive, which means local min) or random (saddle point). (negative definite Hession means local Max)
Here is the best part of the talk, Dr Lee referred to a story of the fall of Constantine in 1543 (actually it’s 1453), and The magician Diorena get the Holy Grail from a sealed stone coffine.
So the local min in low dim maybe just a saddle point in higher dim!!! What’s why we use deeper layers and goes to higher dim
More details of the stoires credited to The three body problem. Respect Da liu :)