MoE and Decoder-Only Transformer code

Summary from this MoE link and this Decoder-only transformer link

1 MoE

In the context of LLMs, MoEs make a simple modification to this architecture: we replace the feed-forward sub-layer with an MoE layer!

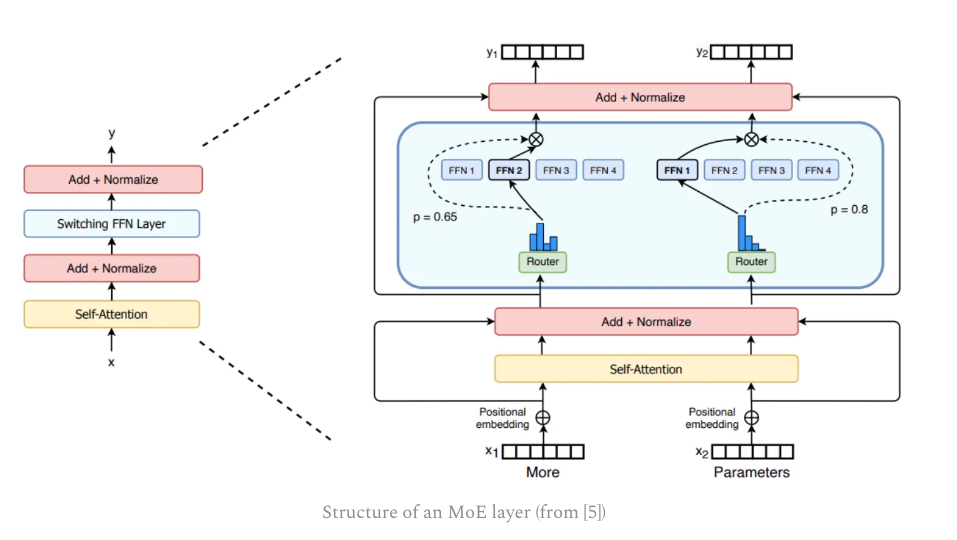
Two primary components:

• Sparse MoE Layer: replaces dense feed-forward layers in the transformer with a sparse layer of several, similarly-structured “experts”.

• Router: determines which tokens in the MoE layer are sent to which experts.

We impose sparsity by only sending a token to its top-K experts. For example, many models set k=1 or k=2, meaning that each token is processed by either one or two experts, respectively.

2 Mixtral-8x7B MoE

7B Mistral-7B LLM, replace each of its FFSL with MoE layer with EIGHT experts, where TWO experts are activated for each token.

In total, 47B parameters
Inference cost, 14B parameters.

3 Attention block

Batch size: $B$
Sequence length: $T$
token vector dimension: $d$
Num of head: $H$

• Set up Q/K/V matrix ```python

  3x dim b/c it includes q/k/v

  self.c_attn = nn.Linear(d, 3*d, bias=bias)

split the output into separate query, key, and value tensors

q, k, v = self.c_attn(x).split(self.d, dim=2) # [B, T, d]

reshape tensor into sequences of smaller token vectors for each head

k = k.view(B, T, self.H, self.d // self.H).transpose(1, 2) # [B, H, T, d // H] q = q.view(B, T, self.H, self.d // self.H).transpose(1, 2) v = v.view(B, T, self.H, self.d // self.H).transpose(1, 2)

- Compute the attention matrix, perform masking and apply dropout
```python
# [B,H,T,d//H] @ [B,H,d//H,T] ->[B,H,T,T]
# k.size(-1) -> d//H
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1))) # [B, H, T, T]
# Apply masking
att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
att = F.softmax(att, dim=-1)
att = self.attn_dropout(att)

• Compute output vectors ```python

  [B,H,T,T]@[B,H,T,d//H]

  y = att @ v # [B, H, T, d // H]

concatenate outputs from each attention head and linearly project

y = y.transpose(1, 2).contiguous().view(B, T, self.d) # [B,T,d]

self.c_proj = nn.Linear(d, d, bias=bias)

y = self.resid_dropout(self.c_proj(y))

## 4 Normalization, Feed-Forward and Residual connect
Different type of normalization, it's all about which mean and standard deviation to use. 
```python
for i in range(nlayers):
    # The normalization
    output = (output - torch.mean(output)) / torch.std(output)

    # # For each NN layer, multiply the vector by the matrix
    output = weight_matrix @ output

The layer-norm is modified with an affine transformation as below THe point-wise Feed-Forward network is defined as below

def forward(self, x):
    #self.c_fc    = nn.Linear(d, 4 * d, bias=bias)
    x = self.c_fc(x) # [B, T, 4*d]
    #self.gelu    = nn.GELU()
    x = self.gelu(x)
    #self.c_proj  = nn.Linear(4 * d, d, bias=bias)
    x = self.c_proj(x) # [B, T, d]
    #self.dropout = nn.Dropout(dropout)
    x = self.dropout(x)
    return x

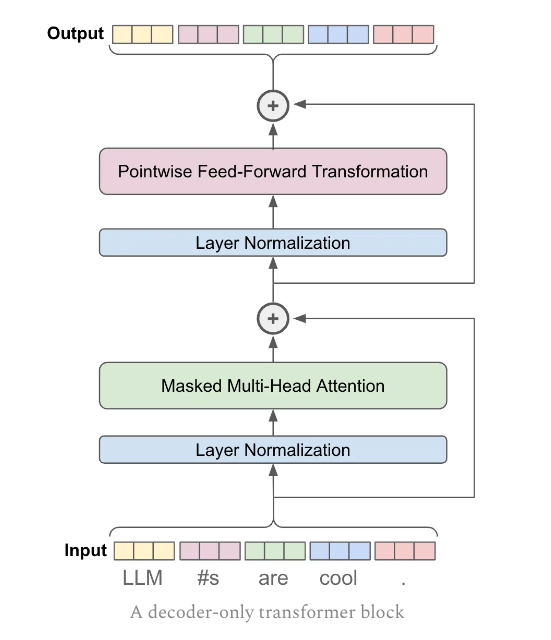
The Resi-Net code is straightfoward

def forward(self, x):
  #self.ln_1 = nn.LayerNorm(d)
  #self.attn is the attention block 
  x = x + self.attn(self.ln_1(x))
  #self.ln_2 = nn.LayerNorm(d)
  #self.ffnn is the feed-forward NN
  x = x + self.ffnn(self.ln_2(x))
  return x

Now we complete following figure for decoder block.

5 Adding Embedding layers

• The token embedding layer is just a mtrix with size [V, d], where V is the size of the tokenizers’ vocabulary. We can simply lookup the token’s embedding from the matrix. It’s impleted by Torch simple lookup table API nn.Embedding(num_embeddings, embedding_dim)

  # wte=nn.Embedding(V, d), # token embeddings
  # idx.size() == [B, T]
  # For each idx, will generate a size-d vector
  tok_emb = self.transformer.wte(idx) # [B, T, d]
  

• The position embedding layers.

  # wpe=nn.Embedding(T, d), # position embeddings
  # pos = torch.arange(0, T, dtype=torch.long, device=device) # [T]
  # For each pos, will generate a size-d vector
  pos_emb = self.transformer.wpe(pos) # [T, d]
  

The input is the summation of these two ` x = self.transformer.drop(tok_emb + pos_emb) ` and the training or inference code is as below

 # pass through all decoder-only blocks
for block in self.transformer.blocks:
    x = block(x)
x = self.transformer.ln_f(x) # final layer norm

if targets is not None:
    # compute the loss if we are given targets
    # head=nn.Linear(d, V, bias=bias)
    logits = self.transformer.head(x)
    loss = F.cross_entropy(
        logits.view(-1, logits.size(-1)),
        targets.view(-1),
        ignore_index=-1,
    )
else:
    # only look at last token if performing inference
    logits = self.transformer.head(x[:, [-1], :])
    loss = None

return logits, loss

Here is the whole picture now