Poisson and Exponential Distribution

马同学(Student Horse) is a great source of math concept clarifictions, both in linear algebra and statistics. I came across this explanantion for both Poisson and Exponential distribution before, and now Im taking some notes for quick reviews.

1, Poisson is the limit of Binomial Distribution

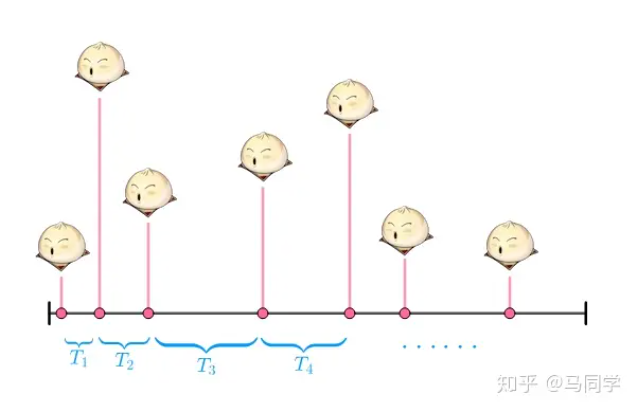
The bun example is a great explanation of this. Assume you sell 3 buns in a day, and you cut one day into 4 periods, then each period is sell or no sell (Piegeon hole theory).

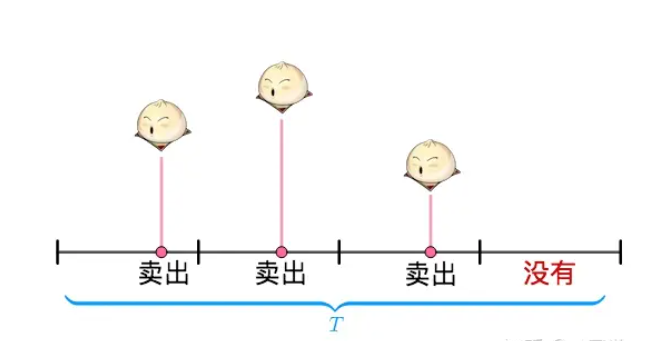
Then you sell more buns, each period may not be binary for 4 periods, then cut them into more finer periods, and the prop is calculated below.

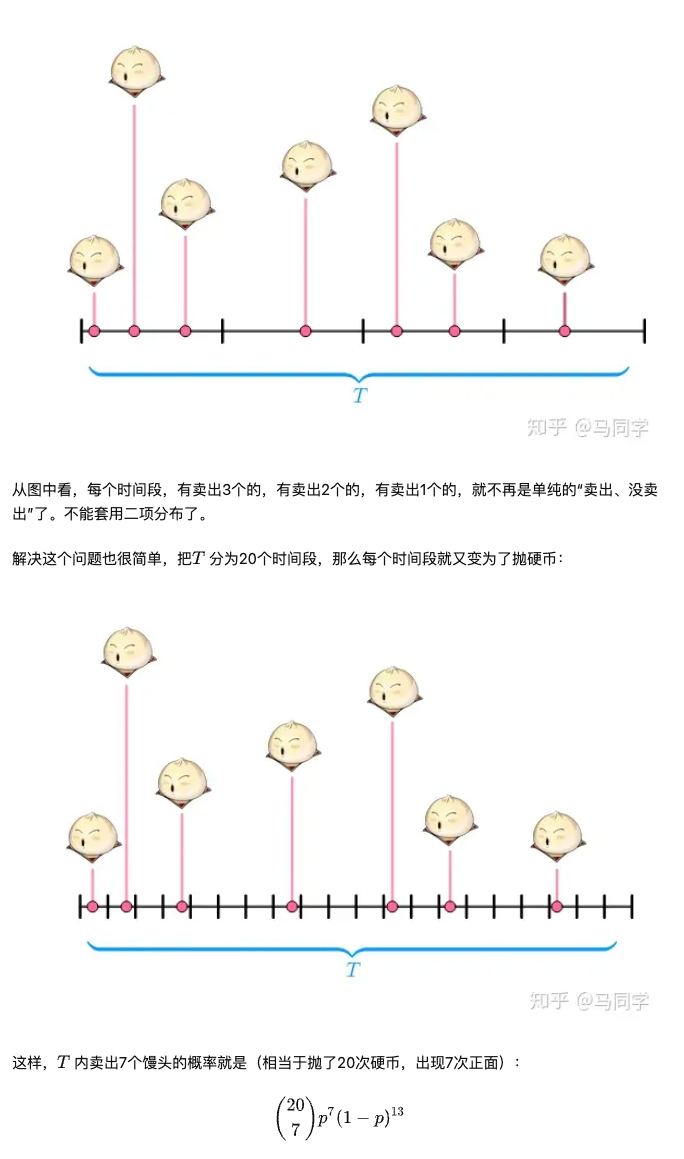
This method will hold true if we let the number of segments, $n$ goes to infinity, then we garantee each segment is binary sell or no sell. And the prop. for sell $p$, is the average number of sold buns $\mu$ divided by $n$.

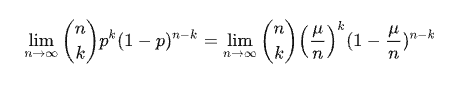
Replace $\mu$ with $\lambda$, we have the standard Poisson formula.

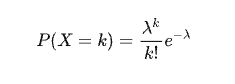
Again, $\lambda$ is the average number of sold buns. and $k$ is actually number of sold buns.

2 Exponential

Now let’s take a look at another problm, what’s the time interval between each bun sell. It’s a stachastic continuous variable. If we have no buns sold on Wedn., so the gap between Tuesday and Thursday has to be larger than one day.

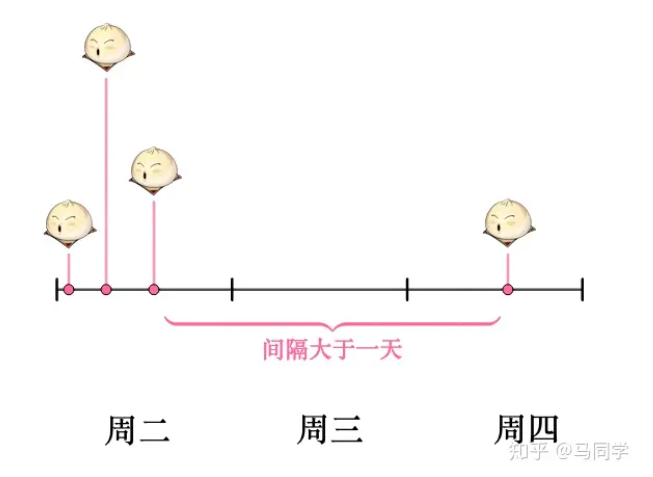
So here is a key idea, the prop. of interval larger than one day, equals to the prop. of no sell on certain day, which can be calculated by Poisson distribution by setting $k$ to zero.

Here we extend Poisson Distribition to Poisson Process, which is adding one more parameter $t$ to define a time period. $t=1$ mean we discuss by daily, and $t=1/8$ is 3 hours.

So the prop. for selling interval larger than a certain time can be expanded based on Poisson process, and one more step gives us the prop. of selling interval smaller than a given time $t$

3 Summary