SmoothQuant and AWQ (,and GPTQ)

GO through LLM Quantization technologies, mainly from Han’s group in MIT

0 Quantization basic

Quantization is nothing more about scaling. After getting the range of the original FL32 data, by calibration, we scale down the data and remap to a low bits range. \(Q(w)=\Delta*Round(\frac{w}{\Delta}) \\ \Delta= \frac{\max{(w)}}{2^{N-1}}\) Another concept is activation, which is actually input $X$ instead of activation functions. In $Q=W_qX$, $X$ is the activation of weight $W_q$

1 SmoothQuan

Han introduced this method in this video and zhihu and paper are very helpful as well.

One formula explained all
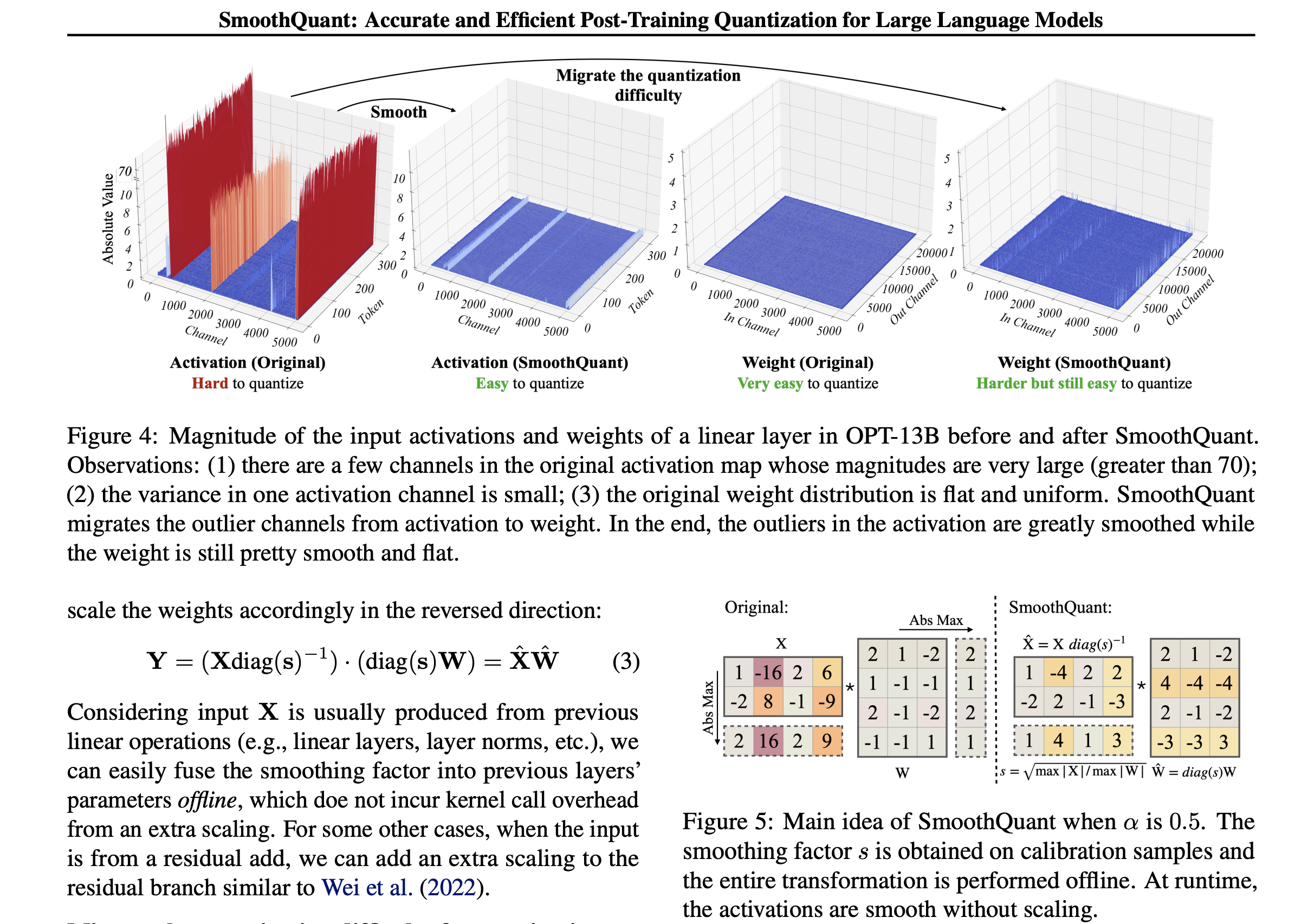
$Y=(Xdiag(s)^{-1})(diag(s)W)=\hat{X}\hat{W}$

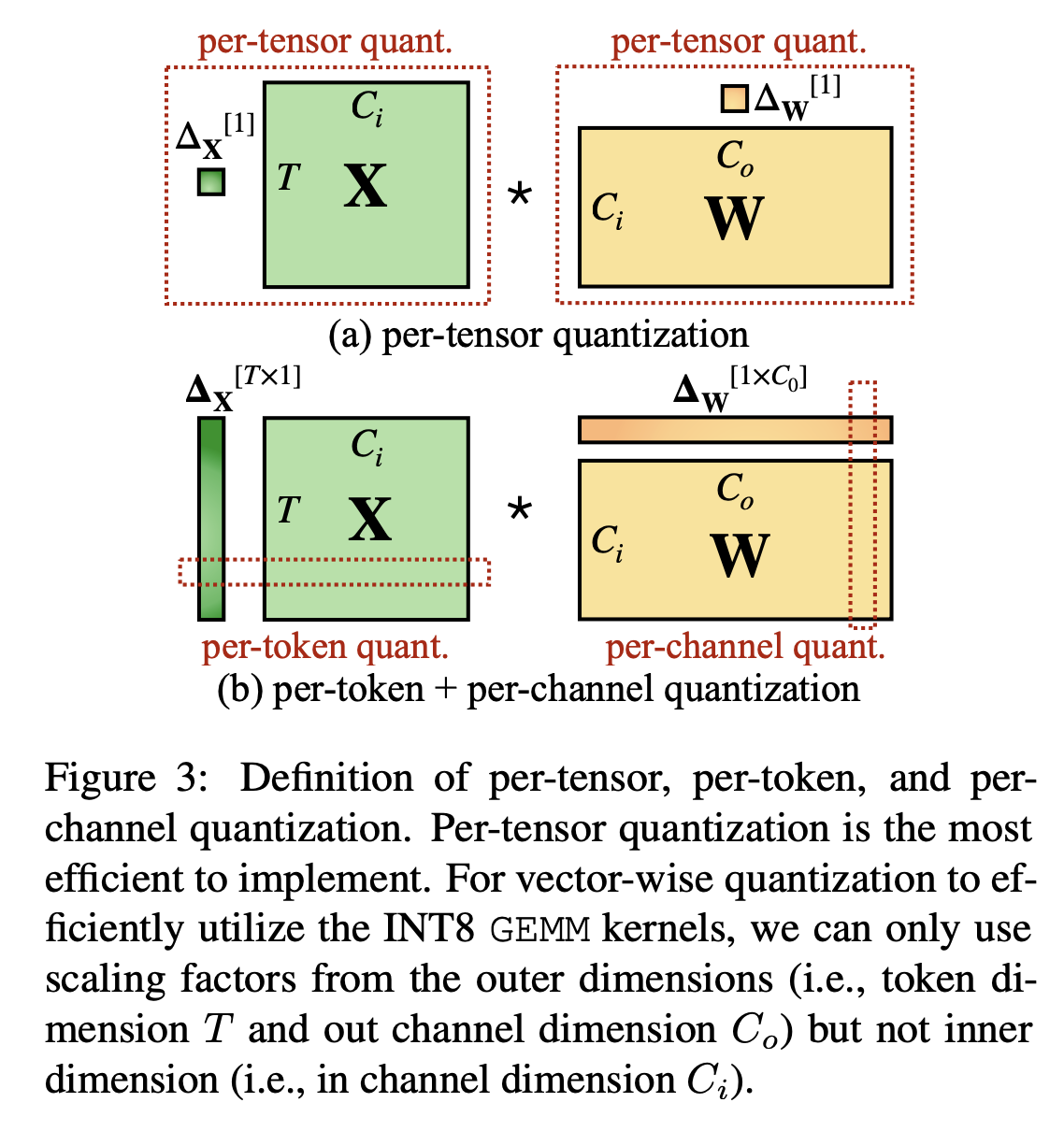
The key challenge is that activation has larger dynamic range and hard to quantize. 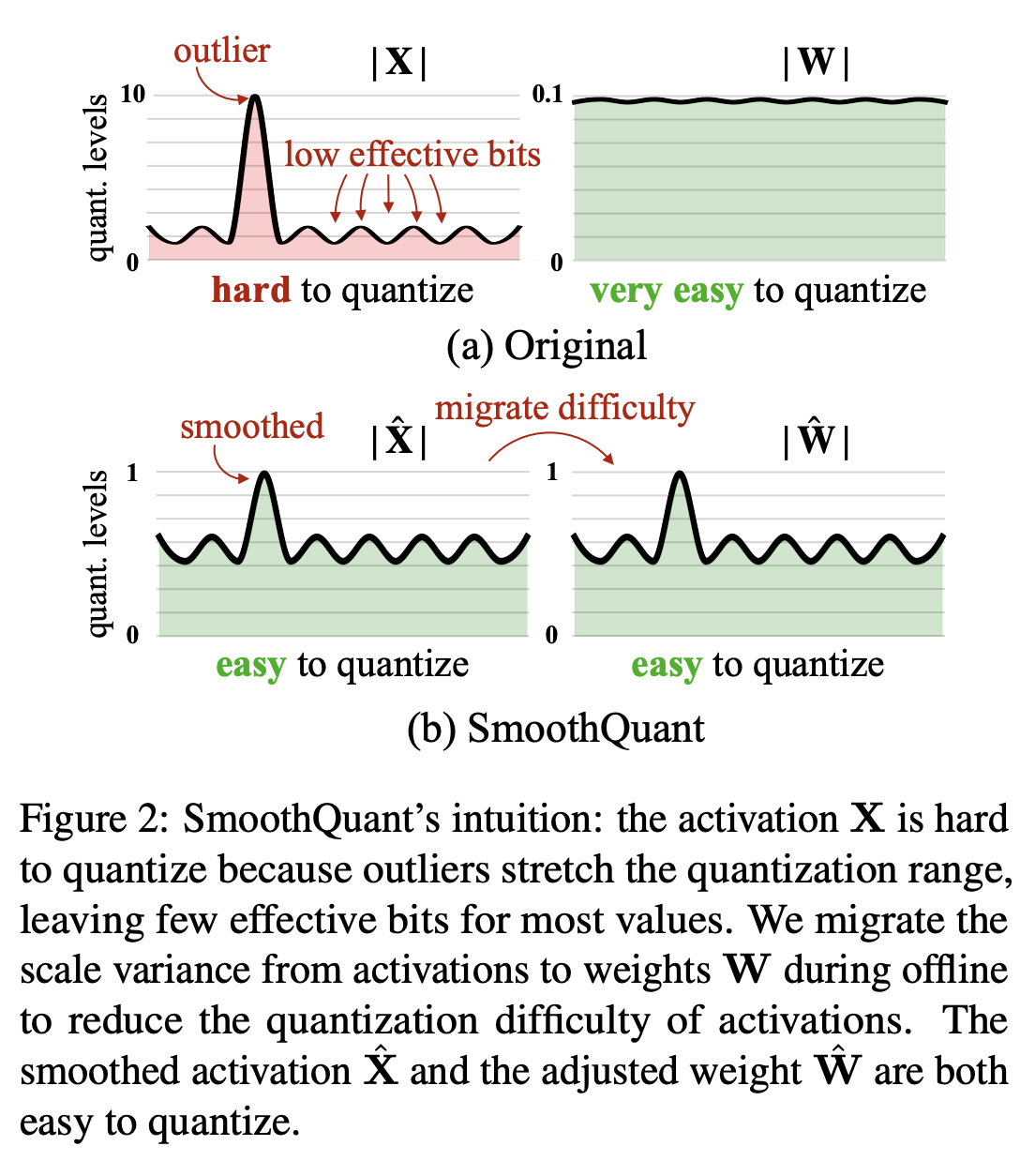So instead of per-tensor quantization, we can consider per-token and per-channel quantization. The outliners are mainly concentrated in certain channels. So we can shift them into weights

2 AWQ

This is 4-bit quantization also from Han’s group, and here are Han’s talk, zhihu(really good explanations), and paper

The goal is to get weight only quantization for single-batch LLM performance. (W8A8 only good for batch serving)

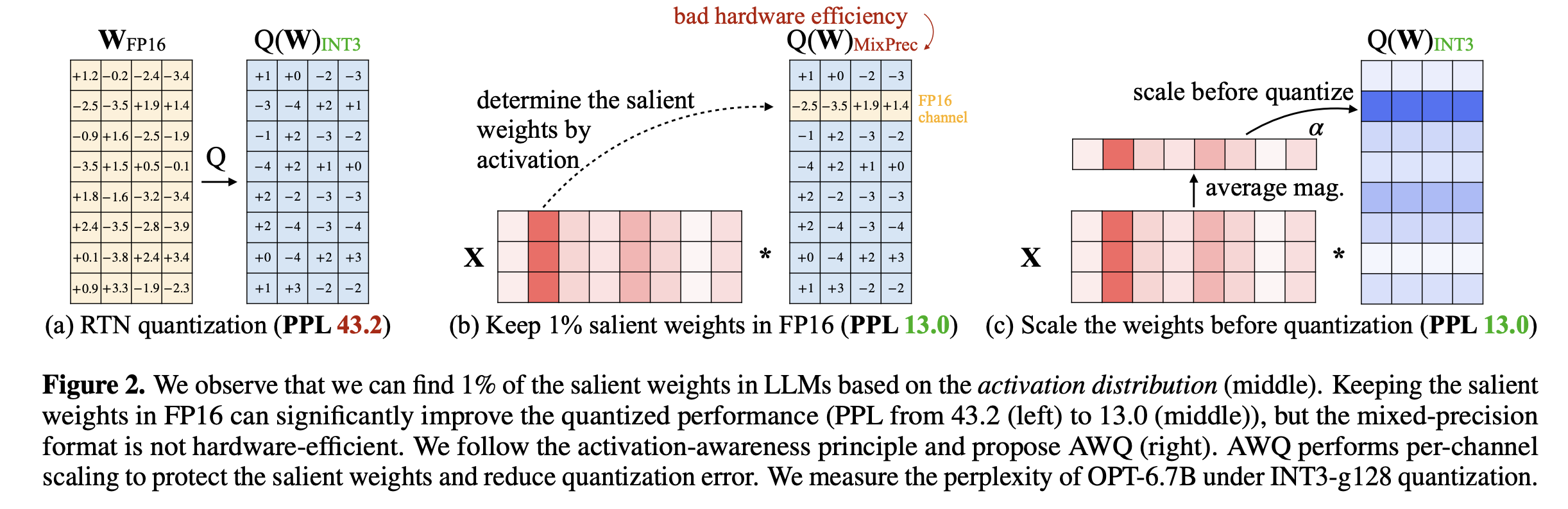
1. Only 1% of salient weight is important for the results. and the paper found out choosing the salient weight based on weight is similar to random choosing. So Activation-aware selection method is used.

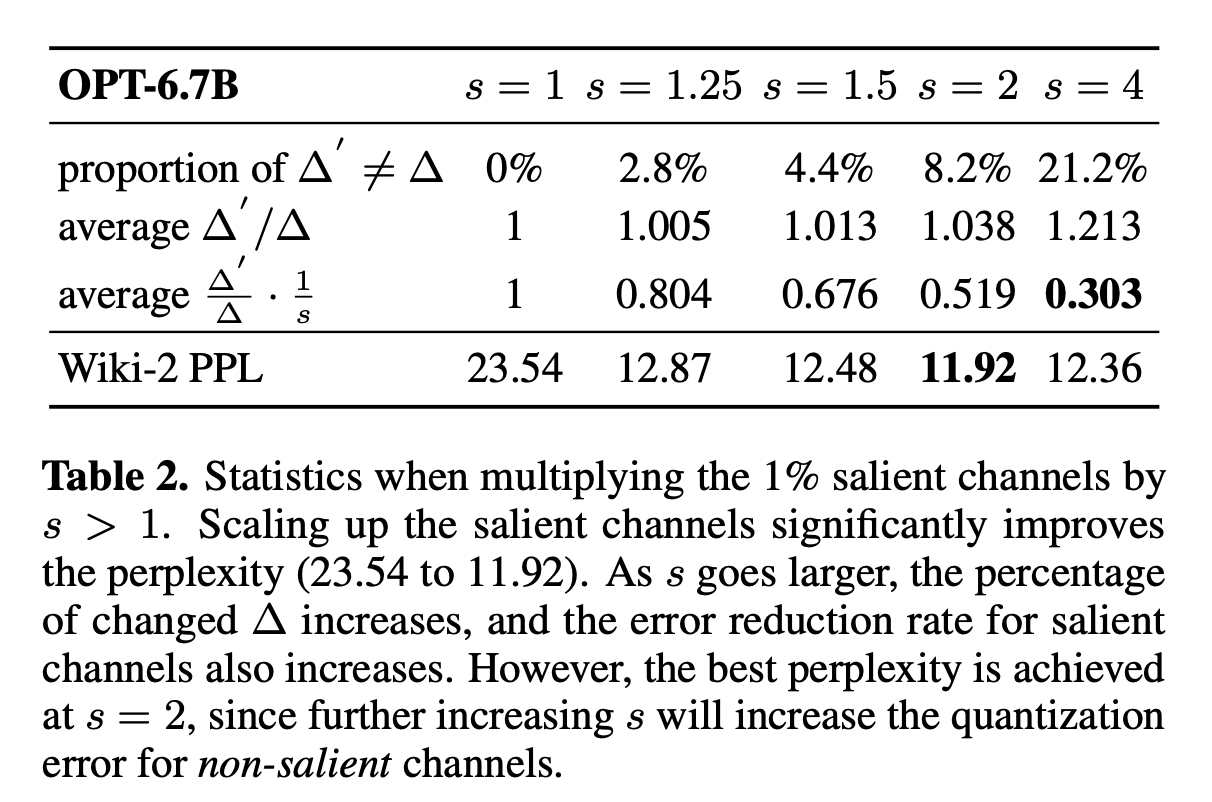
2. The paper noticed that scale up the salient weight and reduce the quantization error, which is a key contribution. Here is the induction: Similar to SmoothQuan, we can scale up weight and scale down the activation
   \(Q(w*s)x/s=\Delta^\prime*Round(\frac{w*s}) \\ \Delta^\prime=\frac{\max{(w*s)}}{2^{N-1}}\)

Based on empirical findings, the error is propotional to $\frac{1}{s}$ and a test shows s=2 gives the best result while larger s would increase non-salient weight error

1. The calculation of the scaling factor can NOT use SGD due to round functino is not differentiable. A grid search is used here for a simplied factor $\alpha$ The source code can be found here

 n_grid = 20
history = []

org_sd = {k: v.cpu() for k, v in block.state_dict().items()}
for ratio in range(n_grid):
    ratio = ratio * 1 / n_grid
    scales = x_max.pow(ratio).clamp(min=1e-4).view(-1)
    scales = scales / (scales.max() * scales.min()).sqrt()

You can see that the ratio $\alpha$ is searched between 0 and 1 with a step of 0.05. and another scaler is added $s = \frac{s}{\sqrt{max(s)min(s)}}$

1. group_size is a hyperparameter used to share $\alpha$ between number of channels. It’s also shows as INT3_group128 which means 128 channels shares a same scaling factor

So here is the summary of the process

3 GPTQ