Reinforcement Learning - Q Learning

Normally we learn RL from Q learning, seems most easy to understand. But this lecture goes PD and PPO first, then Q learning. Interesting, reminds me of linear algebra course back in college.

Value function

Critic, is one of the concepts that I saw it so many times but didn’t get to know exactly what it is till much later. In this part basically here are two examples of critic, the first one is value function $V^\pi(s)$, pay attention that it is depend on the actor $\pi$ which it evaludated.

So same state can leads to different value function based on different actors evaluated, example from 棋魂 is always a great demonstration.

Q function

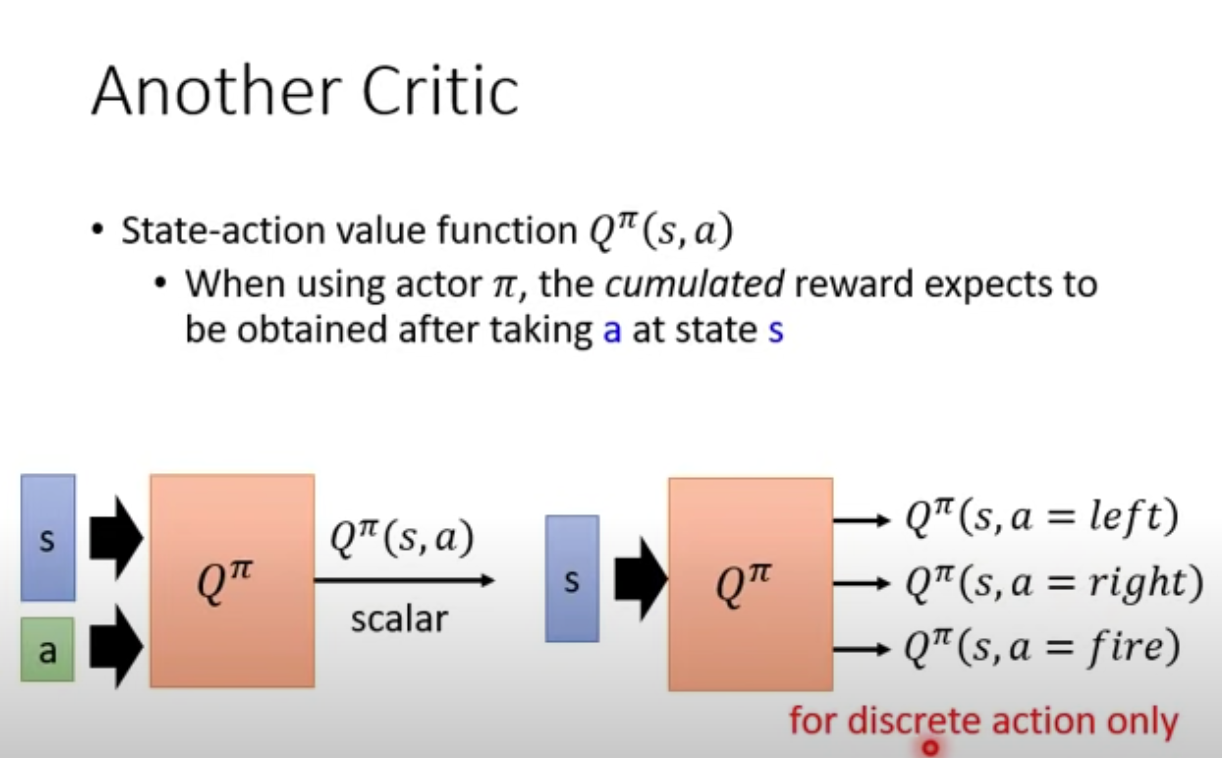
Another example of critic is Q function, which takes in state and action as input, outputs Q values. So Q function is essentially critic!

Two ways of showing the Q function, with 2 inputs(bottom left), or just take state as input and output values based on action.(bottom right, discrete actions only). actor $\pi$ doesn’t have to take action $a$, just force to take action $a$ to get Q function

\[V^\pi(s)=Q^\pi(s,\pi(s))\]

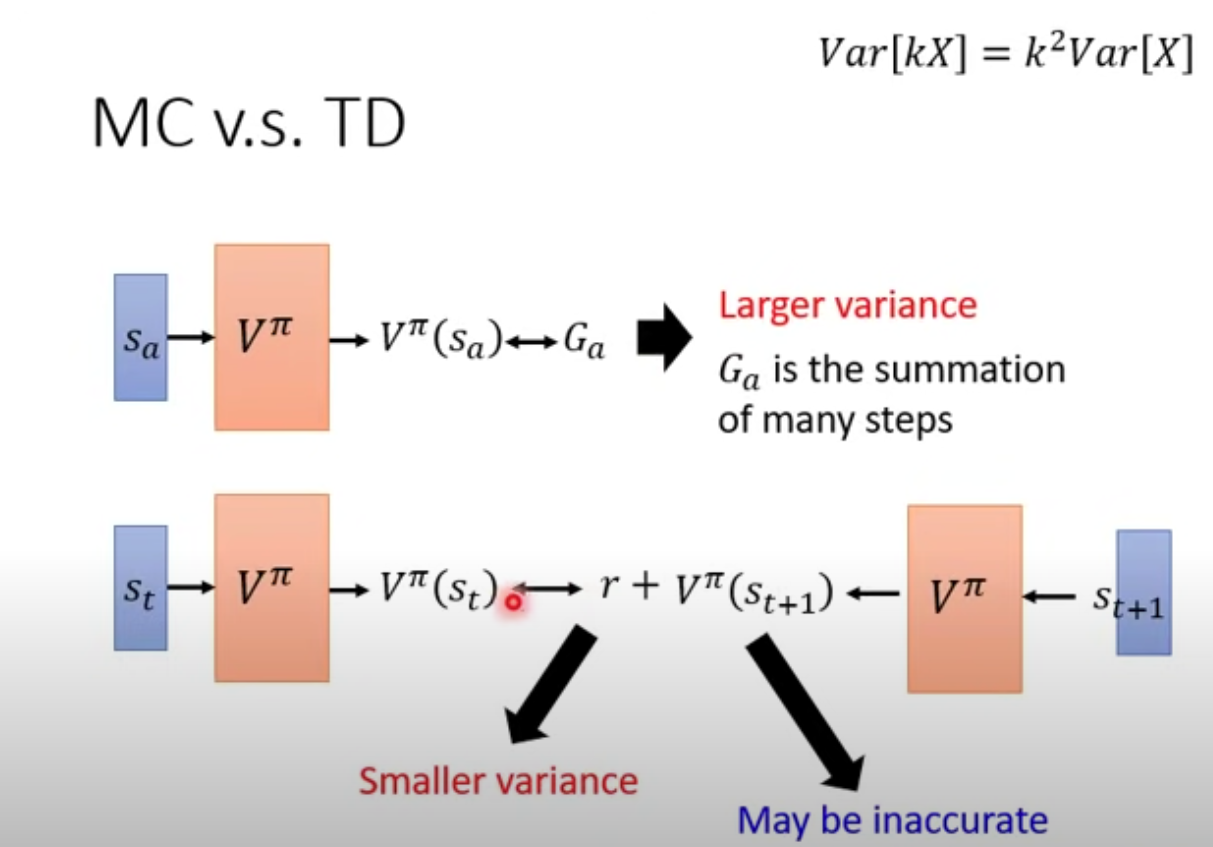
MC vs TD

Let’s go back to value funtion. How can we estimate value functions? Think value function as a NN, you have input state, and as long as you can get the output, you can fit the NN. There are two ways to get output:

1. Monte-Carlo method: calculating the sum of rewards from state $s_a$ all the way to the end of the episode. So you should already know the cons of this method, takes too long to finish the episode. and large variance as well, due to accumulated errors at each step.
2. Temporal-Difference method: It’s much smarter, just take the difference of two consective states $s_t$ and $s_{t+1}$, the groundtruth is reward $r$ at time $t$. The main drawback of this method is low accuracy.
   
   Following example shows two method may get different results.

Q Learning

With Q function, you can implement Q learning as the circle going clockwise. We can guarantee to find a better $\pi’$ than $\pi$ to satisfy the “Better” criterior. Proof skipped but only leave the skeleton as follow:

\(V^\pi(s)=Q^\pi(s,\pi(s))\) \(\le{\max_a}Q^\pi(s,a) = Q^\pi(s,{\pi'}(s))\)