Speculative Decoding

A discussion around tokenizers in slack leads to following comment:
Would be the natural progression after you arrive at the fact taking three steps to get sm art er may be inefficient when there is a high proba it’s going to be smarter

That’s a good explanation of the intuition behind speculative decoding.

1 Speculative Sampling and Speculative Decoding

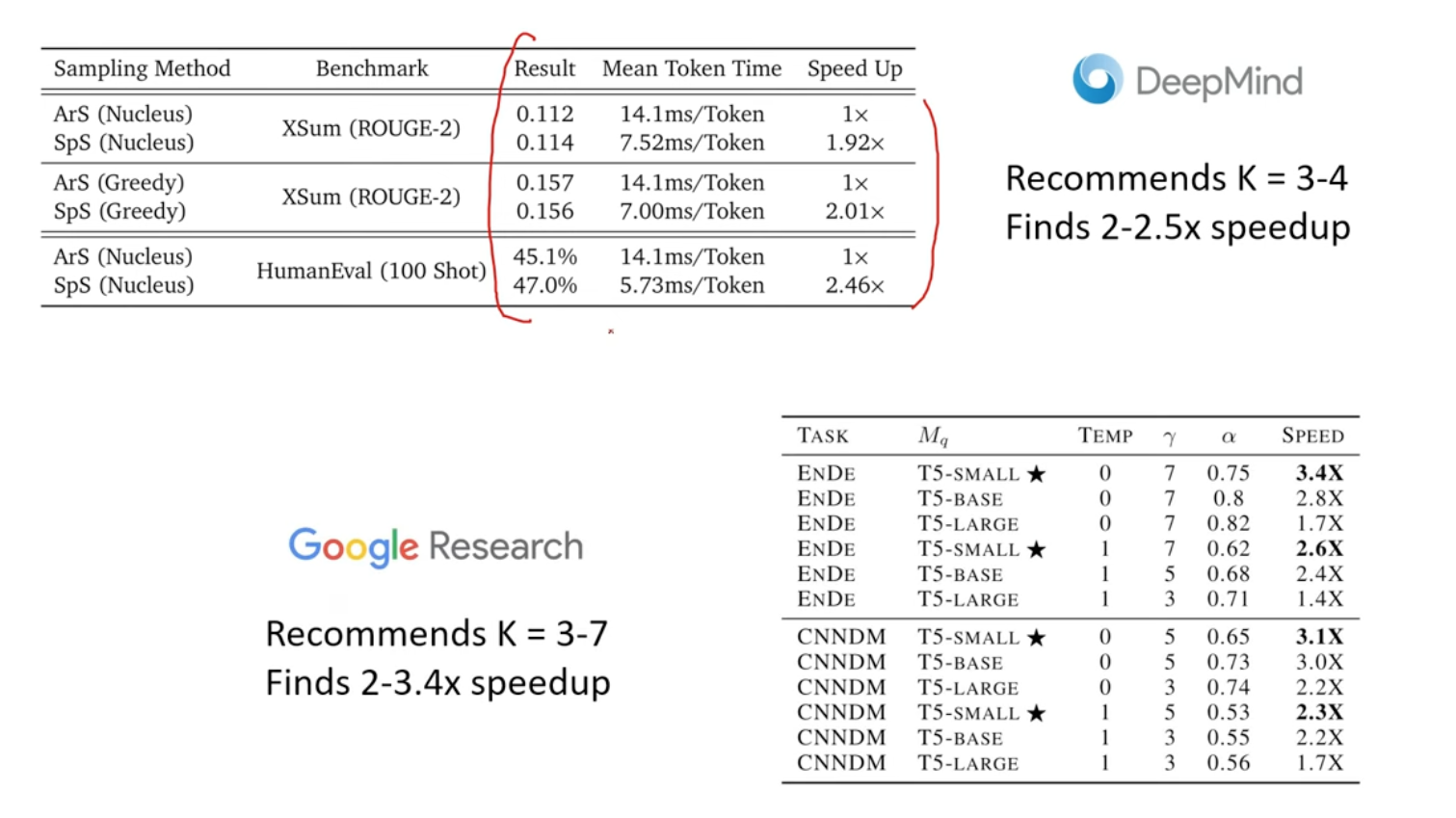
DeepMind and Google published two paper around the same time regarding this algorithm.

Define notations as follow:
$M_p$ = draft model (llama-7b)
$M_q$ = target model (llama-70b)
$pf$ = prefix, $K$ = 5
Do following two steps in parallel.

1. Run draft model for K steps to generate K tokens (generate K distributions over the vacab p(x) and sample out of them)
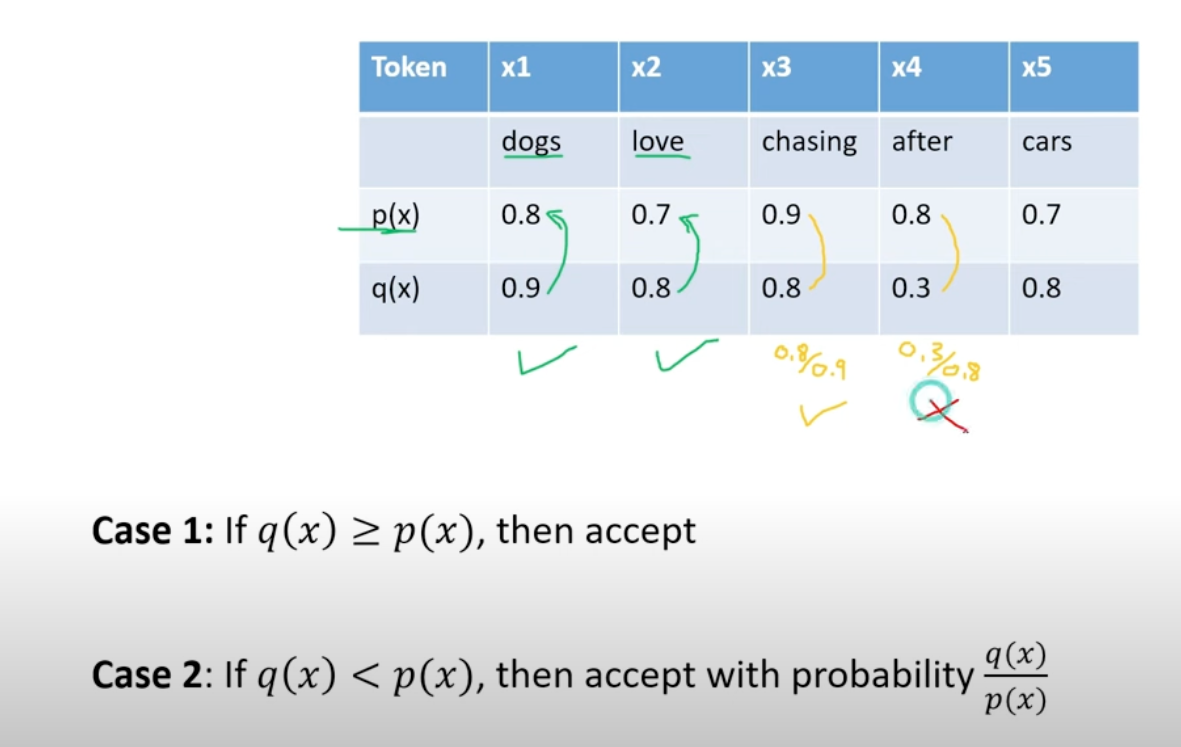
2. Run target model once to get distributions of K+1 tokens (q(x) only, No sampling here) 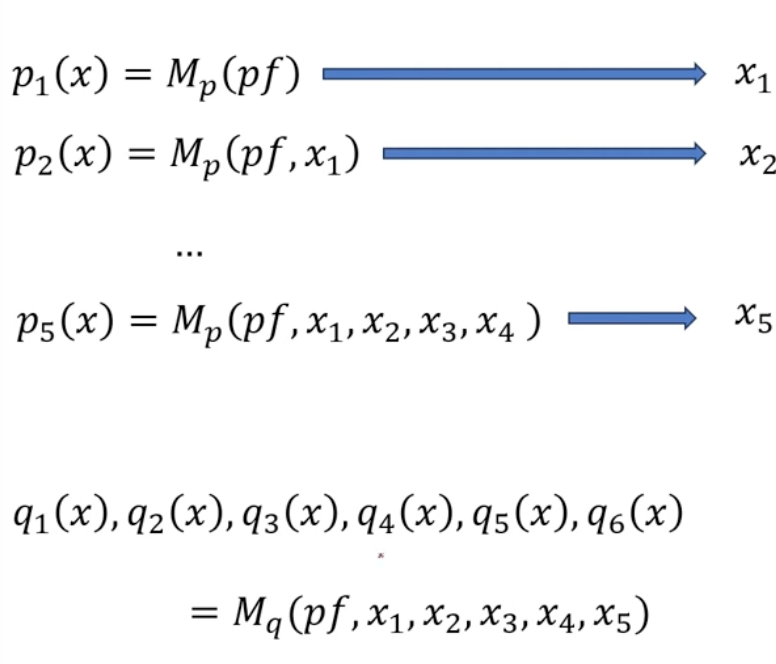The key algorithm is reject sampling, accept or reject tokens based on values of p/q For the first rejected token $i$, we will reject all the token after it and generate token $i$ since we already have $q(i)$, why waste it?

The tricky part is that we are not directly sampling from it, but sample the final token from $(q(x)-p(x))_+$ (The positive part of q(x) minus p(x), the red marked area in the pic below). Why doing it

1. case 1 is area 1
2. case 2 is area 2
3. With red marked area, we covers the whole q distribution.

So doing so can make sure our token distribution is lossless, exactly $q(x)$
This step is important to make sure we generate at least 1 token (When first token is rejected). The worse case is to generate 1 token in each pass, and the best case is to generate K+1 tokens, so speedup is garanteened. (The last token would sample from $q(x)$)

2 Medusa

Tianlei Li from Princeton/Together.ai and Yuhong Li from UIUC published Medusa paper in early 2024.

3 Others

Latest paper from Meta. Similar to Medusa?