Spline 2

Second part of this videos talks about spines again. and I think I found some clue to 1/3 of vel in the previous spine

1 Hermite Spline

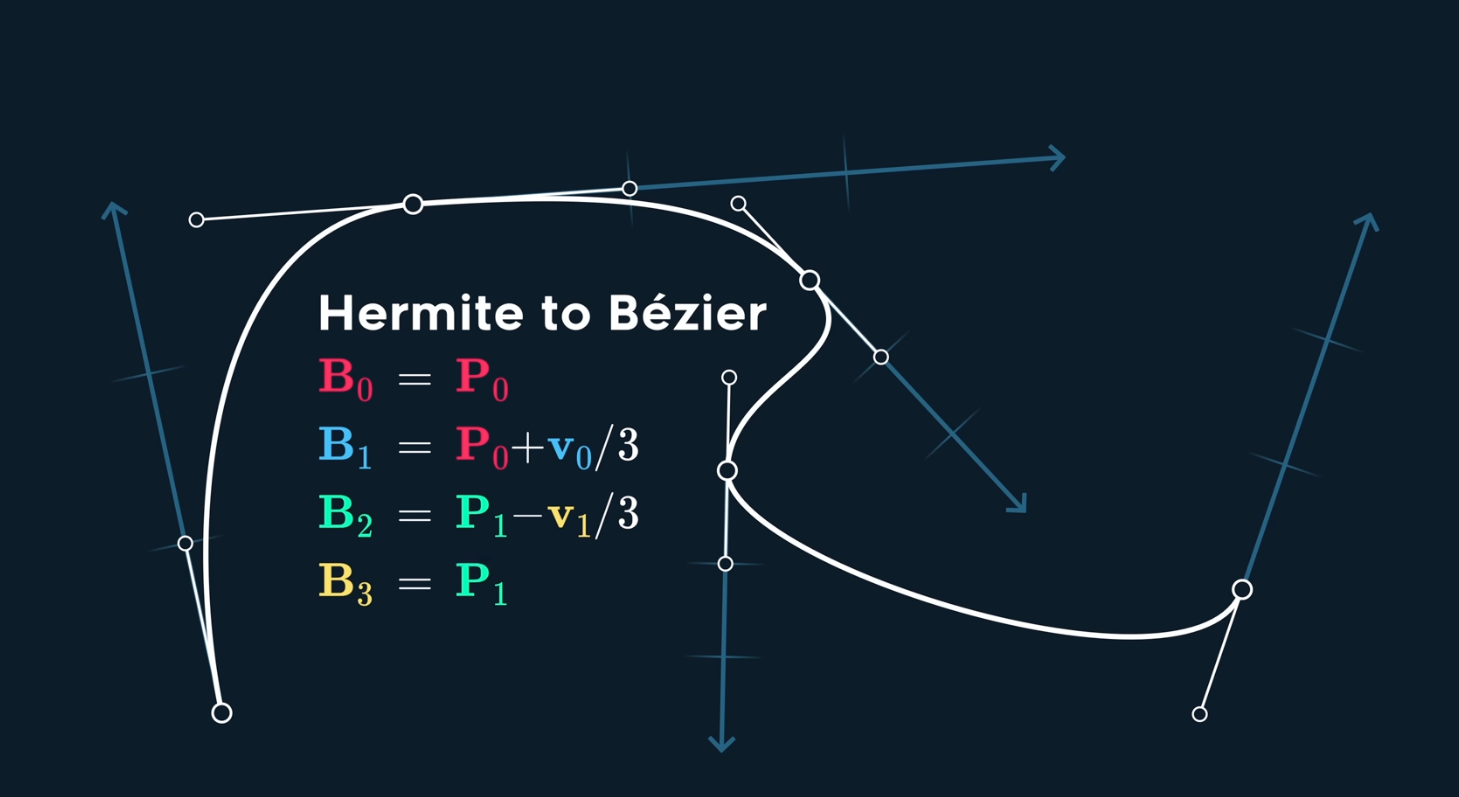
If we define the velocity at each control point, then we get Hermite Spline. 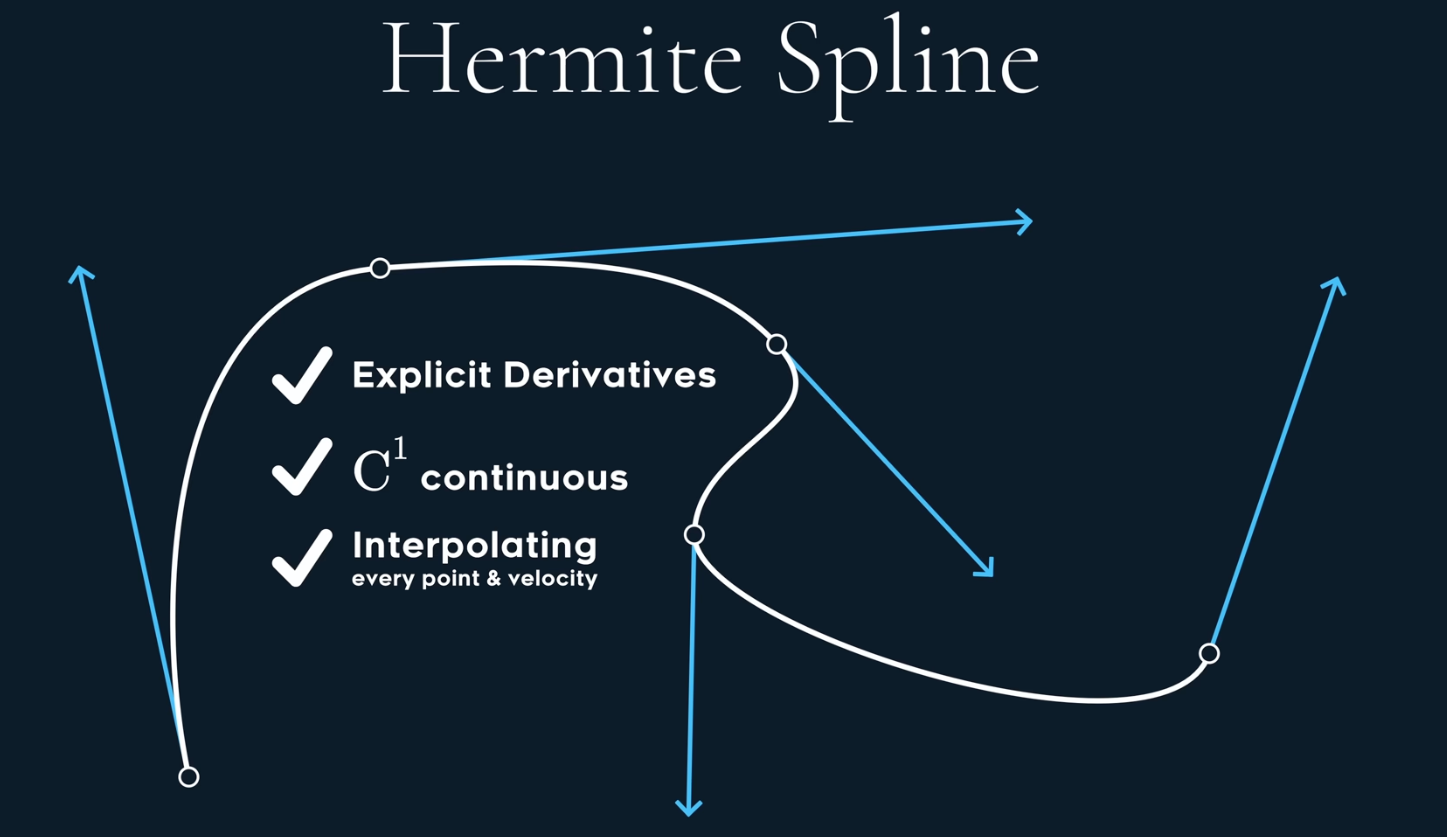and it can be convert to Bezier by adding control points with 1/3 of the velocity manipulations

2 Linear Spline

It’s trivial but cheap

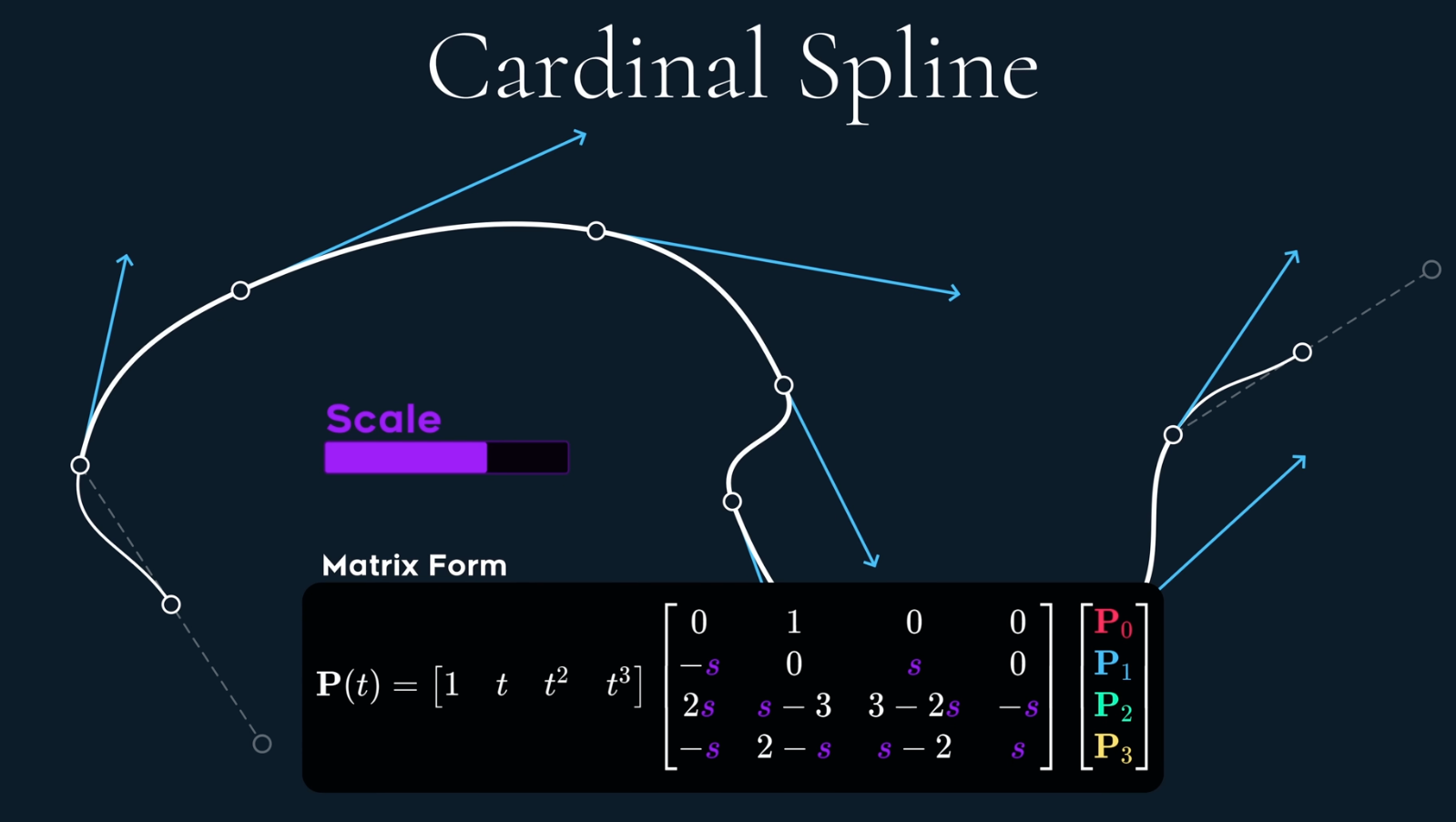
3 Cardinal Spline

On top of Hermite, if we define the velocity is in the direction of adjacent points, we get cardinal spline. The scale is used to control the length of vel. vector. The Catmull-Rom is actually a special type of cardinal spline with scalar $s=0.5$
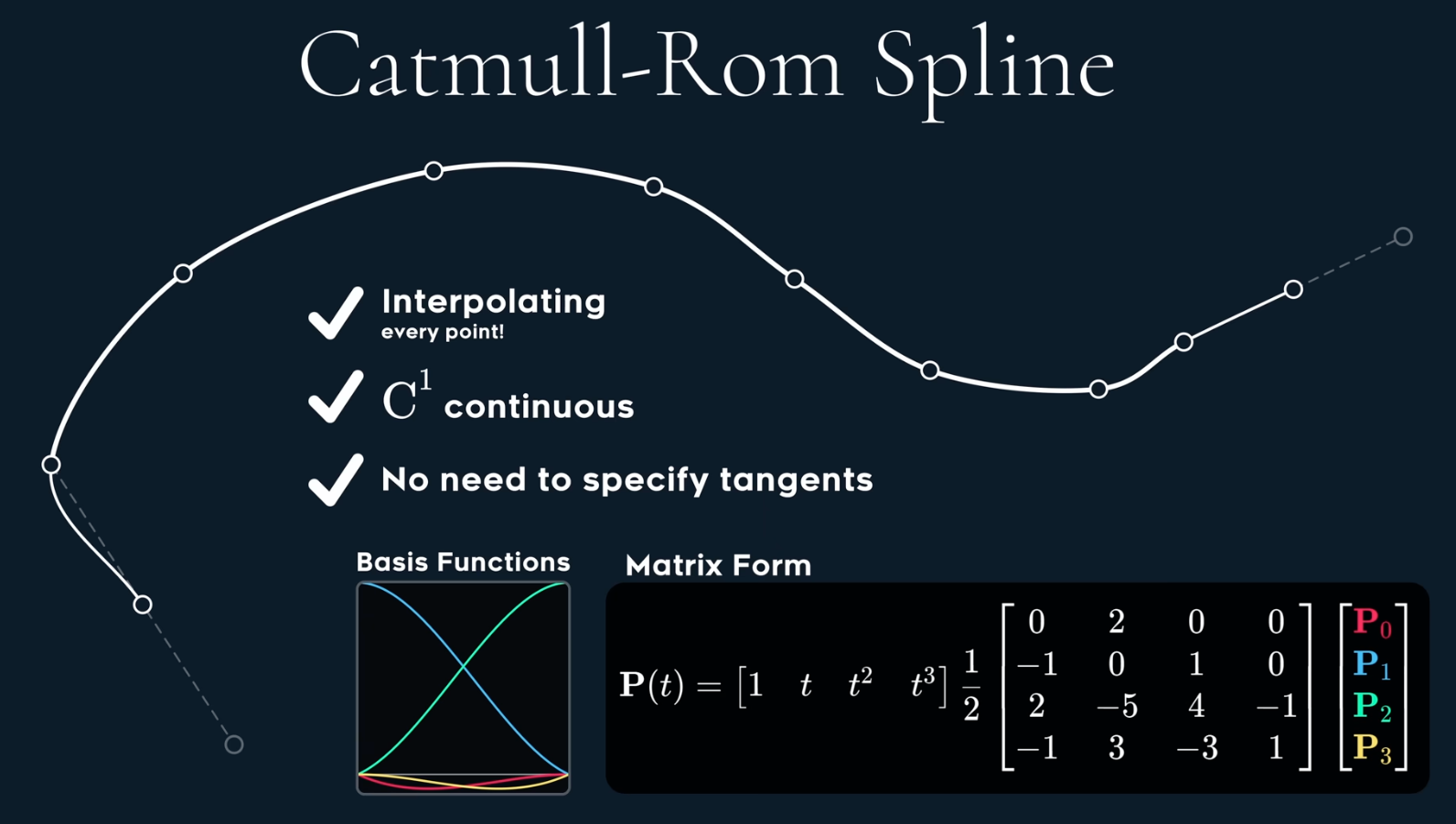
It’s very smooth but still not $C^2$

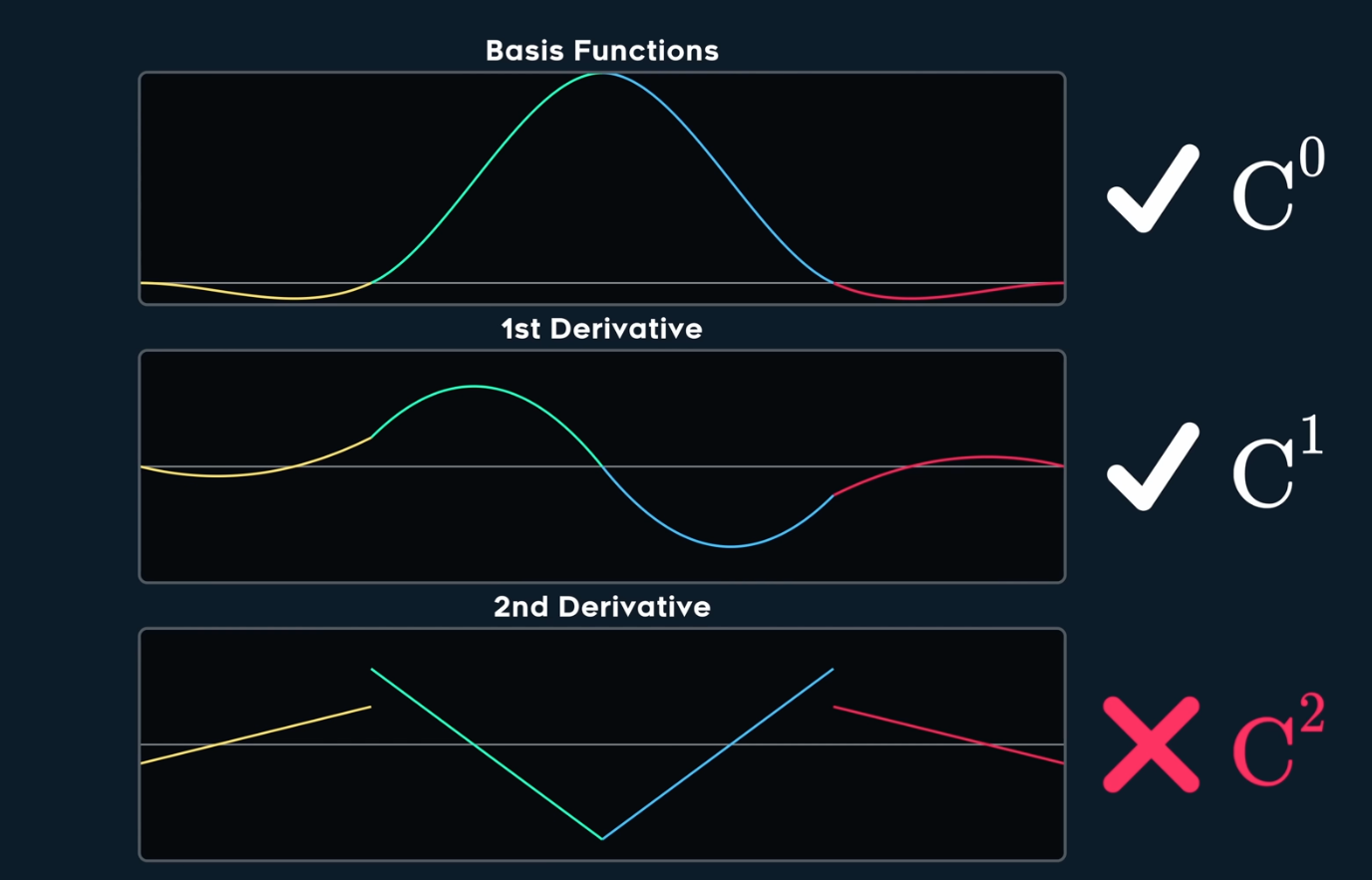
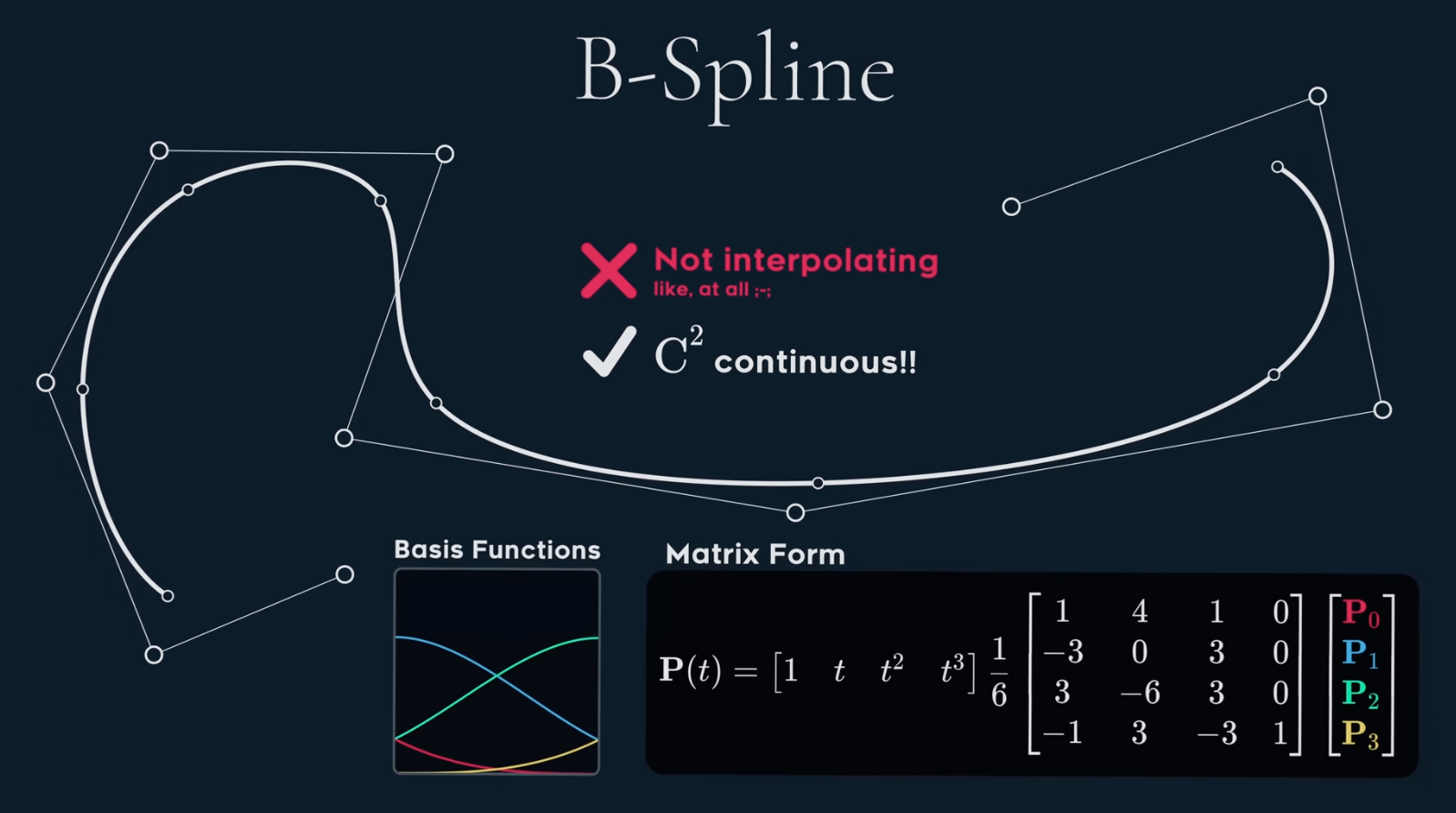
4 B-Spline

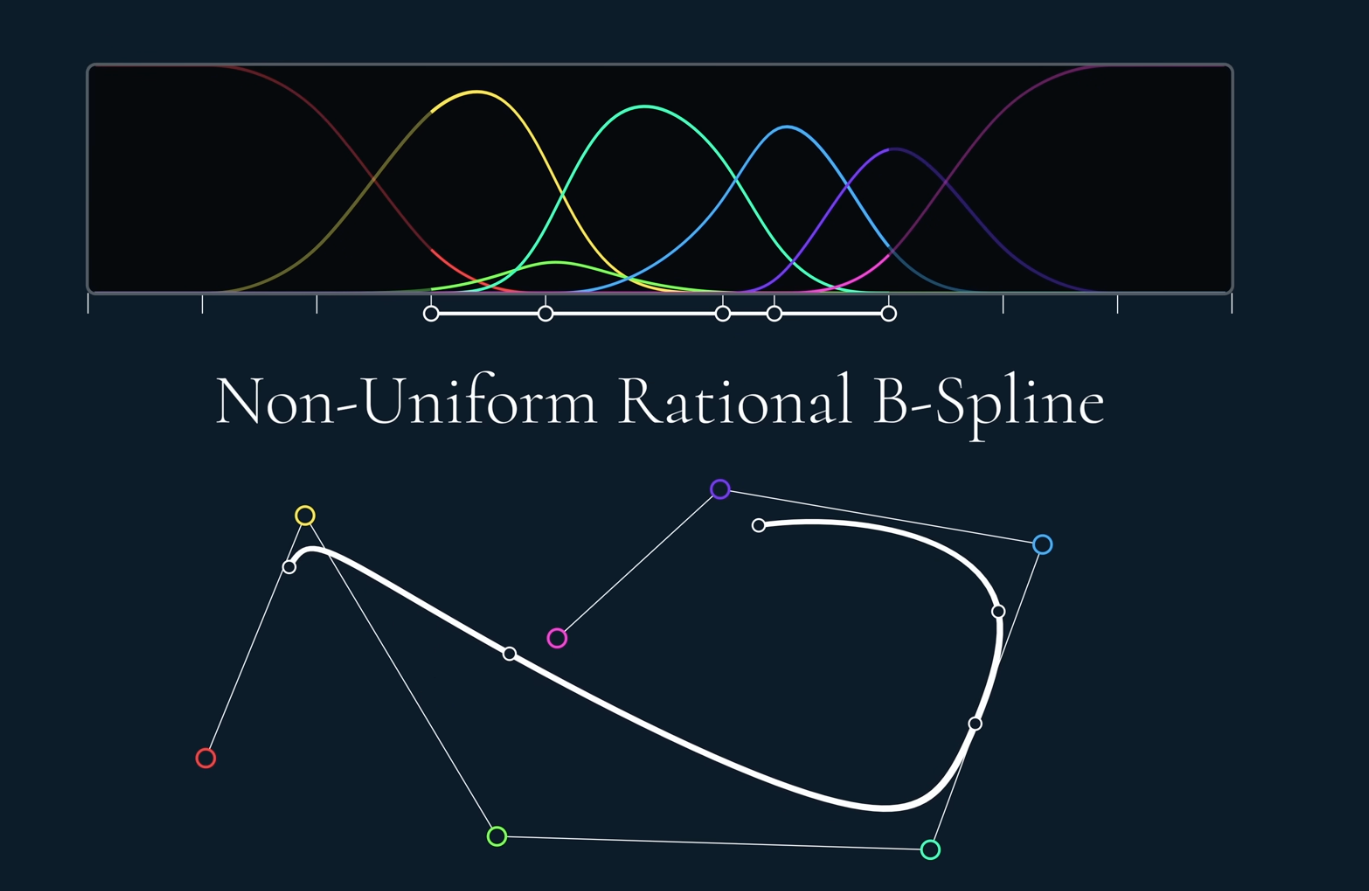
In order to get $C^2$, we solve 16 equations (See details in Spline 1) then we get B-spline and there are other types of B-spline is we change the interval length and give weights to different control points, it’s call NURBS for short.

5 Summary