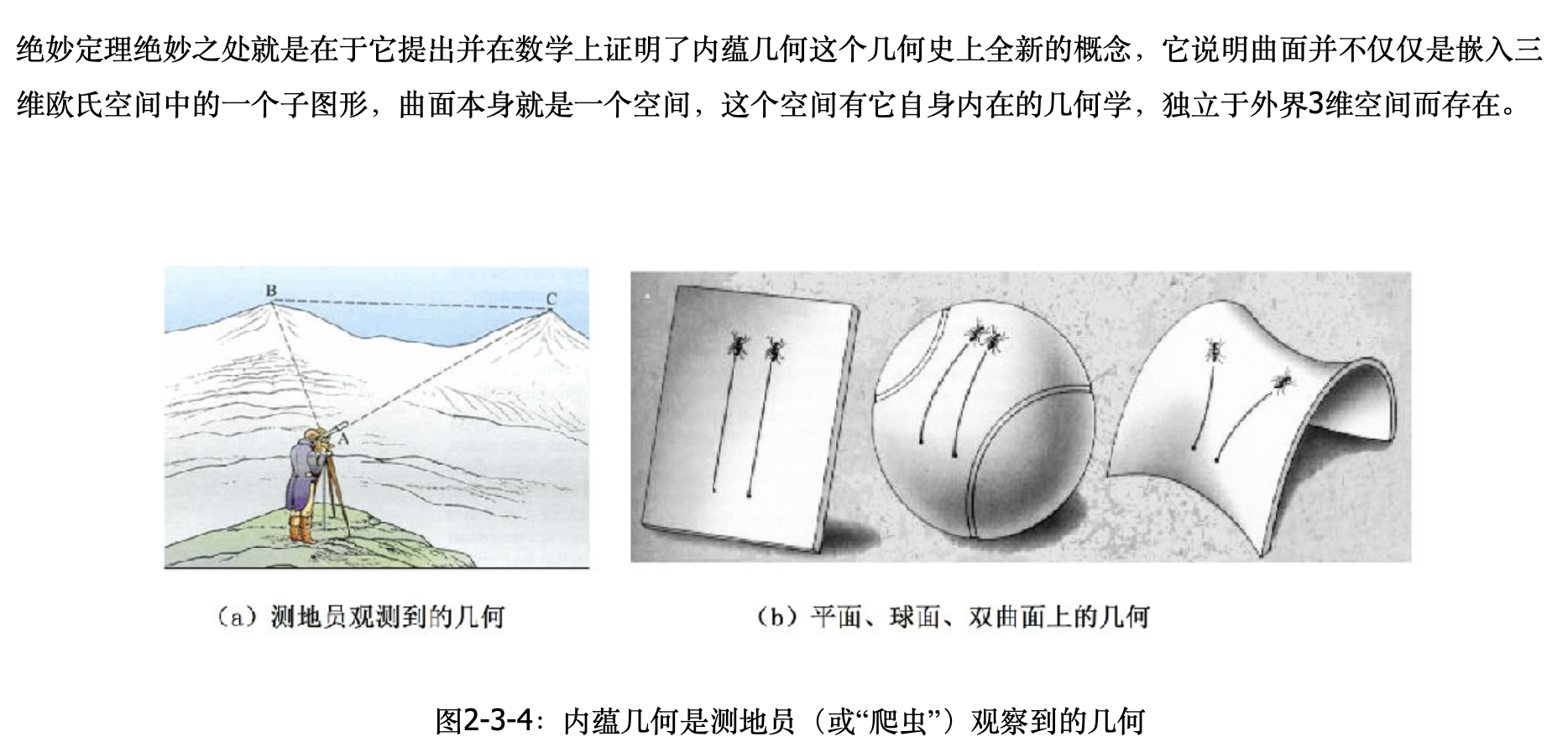
Theorema Egregium

Gauss’s Theorema Egregium, which is Latin for “Remarkable Theorem”, is a major result of differential geometry. I found a good introduction here and video by Yongle Li.

0 Intricint Geometry

The study is about intrinsic geometry. The length of an arch is one example, not changed by curvature or torsion.

1 Review of Curvatures

curvature $\rho$ is the reciprocal of the radius of curvature $K$

There are two principle curvatures, the min and max of all curvs. Defined by Euler in 1760.

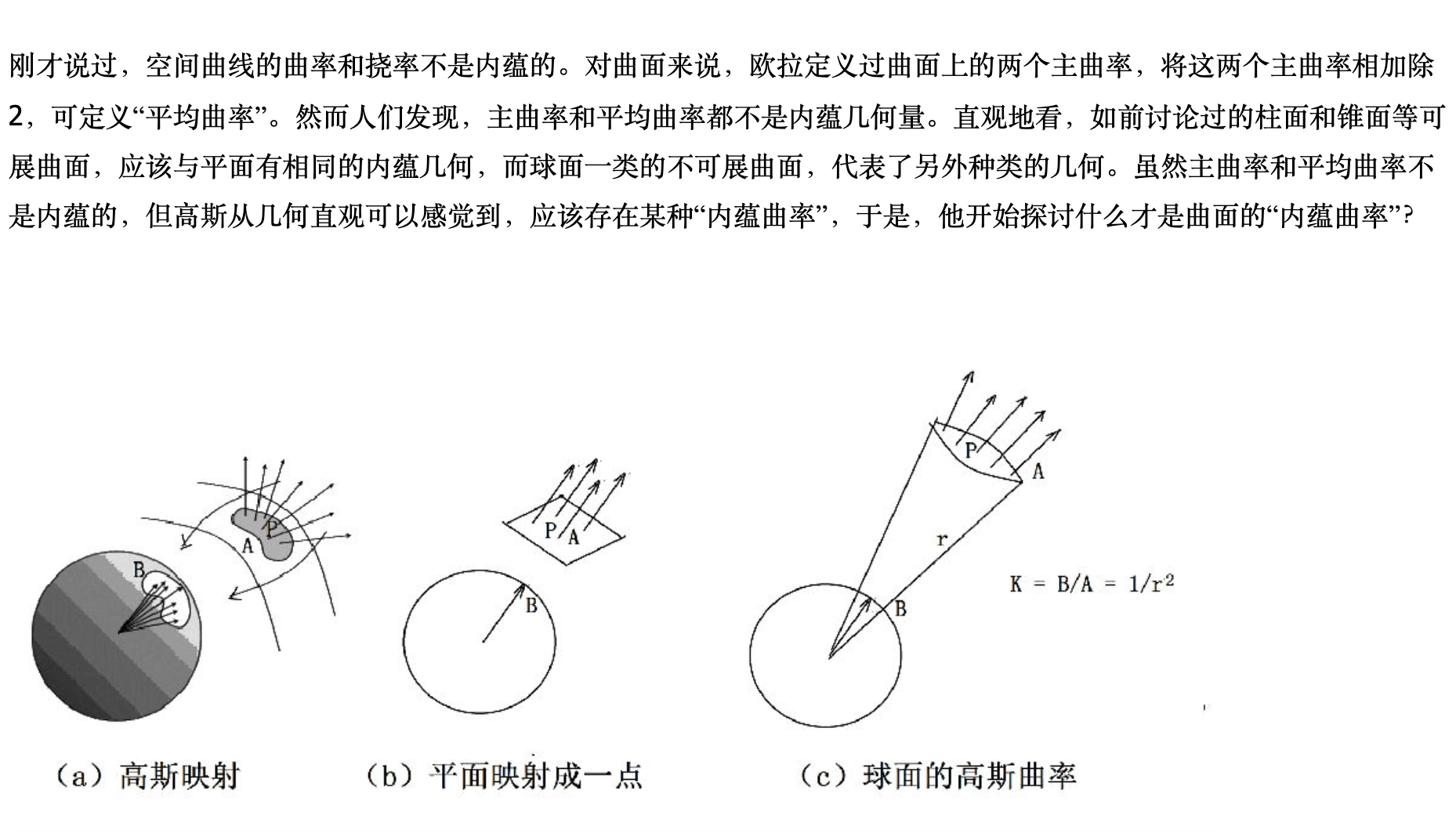
2 Gaussian Curvature

The mean curvature is the mean of principle curvatures, and the gaussian is the multiplication. It’s intrinsic for a surface

The original defination is the ratio of the area of two surfaces.

Theorema Egregium gives birth to intrinsic geometry.